降维技术---PCA

数据计算和结果展示一直是数据挖掘领域的难点，一般情况下，数据都拥有超过三维，维数越多，处理上就越吃力。所以，采用降维技术对数据进行简化一直是数据挖掘工作者感兴趣的方向。

对数据进行简化的好处：使得数据集更易于使用，降低算法的计算开销，去除噪声，使得结果易懂。

主成分分析法（PCA）是一种常用的降维技术。在PCA中，数据从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。

为什么选择最大方差的方向和方差的正交方向？

如果想要画出一条直线，使得直线要尽可能多的覆盖坐标轴中的点，在下图中的三条直线中，B直线为最大方差代表的直线，说明覆盖数据信息最多，C直线为B直线的垂线，它是覆盖数据次大差异性的直线。

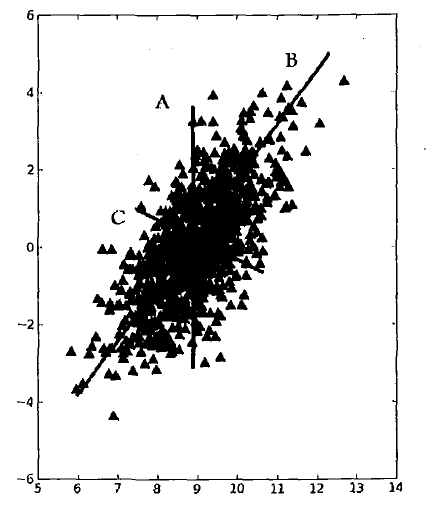
PCA的优点：降低数据的复杂性，识别最重要的多个特征。

PCA的原理：借助于正交变换，将其分量相关的原随机向量转化成其分量不相关的新随机向量。这在代数上表现为将原随机向量的协方差矩阵变换为对角形阵。

PCA的实现：通过对协方差矩阵进行特征分解，以得出数据的主成分（即特征向量）和权值（即特征值）

将原始数据转换成前N个主成分的具体实现步骤：

1.去除平均值

2.计算协方差矩阵

3.计算协方差矩阵的特征值和特征向量

4.将特征值从大到小排序

5.保留最上面的N个特征向量

6.将数据转换到上述N个特征向量构建的新空间中

代码实现

def PCA(dataMatrix, topNFeature=999):
    meanVals = mean(dataMatrix, axis=0)
    meanRemovedMatrix = dataMatrix - meanVals      #1. remove mean

    covMat = cov(meanRemovedMatrix, rowvar=0)      #2. covariance matrix
    eigVals,eigVects = linalg.eig(mat(covMat))     #3. compute matrix eigenvalues and eigenvectors
    eigValInd = argsort(eigVals)                   #4. sort, sort goes smallest to largest
    eigValInd = eigValInd[:-(topNFeature+1):-1]    #5_1 cut off unwanted dimensions
    redEigVects = eigVects[:,eigValInd]            #5_2 reorganize eig vects largest to smallest
    lowDDataMat = meanRemovedMatrix * redEigVects  #6 transform data into new dimensions
    return lowDDataMat