CF1855B Longest Divisors Interval 题解

题意：

给定一个数 \(n\)，求一个连续区间 \([l,r]\) 使得 \(n\) 是区间内每个数的倍数，最大化这个区间的长度(多组数据)。

思路:

逆向思考一波，（

如果一个数 \(x\) 不是 \(n\) 的因数，那么 \(x\) 的倍数不能在区间内。

举个例子，比如 $ n $ 是13，3不是13的因数，\(3,6,9,12\) 也就不可能出现在区间内z，也就是每隔2个数就有一个不能选在区间中。

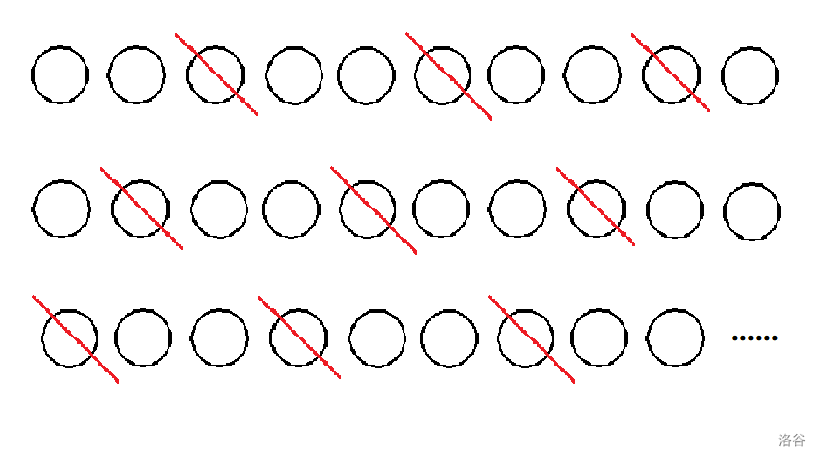
也就是说，一个数 \(x\) 不是 \(n\) 的因数，那么这个区间长度就不可能超过 \(x\)，最长也只能到 \(x-1\)。

我们可以找到 \(1,2,3,4,...\) 中第一个不是 \(n\) 的因数的 \(x\) ,易知 \(1,2,3,...,x-1\) 都是符合要求的数。

既然最长只能到 \(x-1\)，那我们不就可以选择 \([1,x-1]\) 作为答案了。

喜闻乐见的代码时间（

点击查看代码

#include<bits/stdc++.h>
#define fo(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
#define Ts template<typename Ty,typename... Ar>
#define Tp template<typename Ty>
#define isdigit(c) ((c)>='0'&&(c)<='9')
#define ll long long
#define RS register
#define gc getchar
#define pc putchar
#define I inline
using namespace std;
Tp I Ty wmax(Ty a,Ty b){return a>=b? a:b;}
Tp I Ty wmin(Ty a,Ty b){return a<=b? a:b;}
namespace WrongIO
{
	Tp I void read(Ty &x){x=0;Ty opt=1;char c=gc();while(!isdigit(c)&&c!='-')c=gc();if(c=='-')opt=-1,c=gc();while(isdigit(c))x=(x<<3)+(x<<1),x+=c-'0',c=gc();x*=opt;return;}
	Tp I void write(Ty x){short OI_USE[50],OI_top=0;if(x<=0) if(x==0)pc('0');else pc('-'),x*=-1;while(x)OI_USE[++OI_top]=x%10,x/=10;while(OI_top--)pc(OI_USE[OI_top+1]+'0');return;}
    I void writec(char c[]){int len=strlen(c);for(int i=0;i<len;i++)pc(c[i]);}
    I void writes(string s){int len=s.length();for(int i=0;i<len;i++)pc(s[i]);}
    I void readc(char &c,int l,int r){c=gc(); while(c!=EOF&&(c<l||c>r)) c=gc();}
    I void readc(char &c,char val){c=gc();while(c!=EOF&&c!=val) c=gc();}
    I void readc(char val){char c;c=gc();while(c!=EOF&&c!=val) c=gc();}
    I void readls(string &s){char c=gc();while(c!='\n') s.push_back(c),c=gc();}
    Ts I void read(Ty &x,Ar &...y) {read(x),read(y...);}
} using namespace WrongIO;
//这是祖传514年的板子，不用管(
ll T;
int main()
{
	cin>>T;
	while(T--)
	{
		ll n; cin>>n; ll i=1;
		for(;i<=100;i++)
		{
			if(n%i!=0) break;
		}
		write(i-1),pc('\n'); //i即为第一个不是n的因数的数
	}
	return 0;
}

如果样例解释的给出的区间也是 \([1,x-1]\) 就好了（