CF813E Army Creation 题解

题目链接：CF 或者 洛谷

并不是很难的题，关于颜色数量类问题，那么很显然，沿用经典的 "HH的项链" 思想去思考问题。由于涉及到了 \(k\) 个数的限制，我们观察到如果一个数在一个区间上有区间贡献：

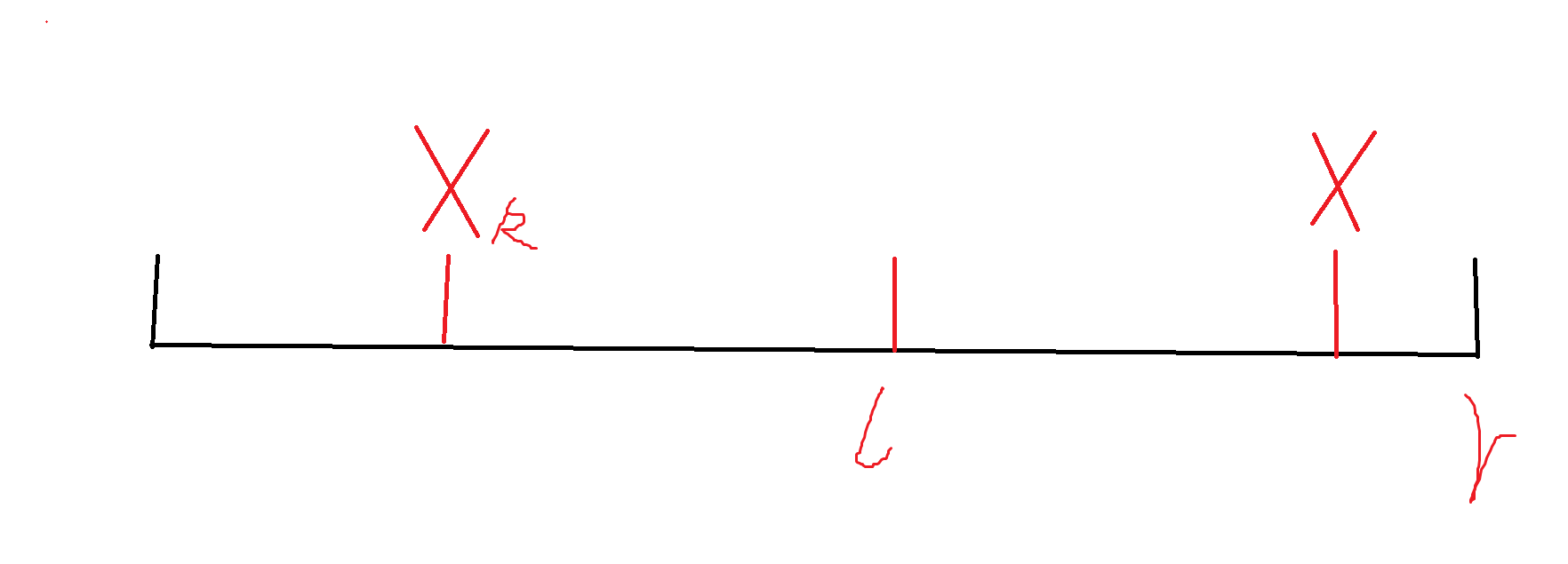
其中 \(x_k\) 表示为当前 \(x\) 的第前 \(k+1\) 个数，换句话来讲，\(x_k\) 到当前的 \(x\) 所在的位置上包括 \(x\) 一共恰好有 \(k\) 个 \(x\)。我们观察到这个 \(x_k<l\) 的时候，可以保证，\([l,r]\) 上至多有 \(k\) 个 \(x\)。这个 \(x\) 显然可以贡献。那么很简单了，这个玩意是可以预处理出来的，问题转化为在 \([l,r]\) 上有多少个 \(pre_k<l\)，这个问题显然无脑树套树解决，但我们注意到这玩意是一个计数类型问题，所以我们可以用主席树优化到单 \(log\)。稍微注意下问的是 \(<l\) 的数量，我们转化为 \(<=l-1\) 的数量，就是常规的主席树了，注意 \(l-1\) 可为 \(0\)，范围别写错了。强制在线注意下 \(l>r\) 需要 \(swap\)。注意 \((pre_k,curr]\) 有 \(k\) 个数，所以我们的 \(pre_k\) 应该是从当前数往前数 \(k\) 个 \(x\) 才对，换句话来说，这是从当前数往左数的第 \(k+1\) 个 \(x\)，如果没有就是 \(0\)。

参照代码

#include <bits/stdc++.h>

// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
// #pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")

// #define isPbdsFile

#ifdef isPbdsFile

#include <bits/extc++.h>

#else

#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>

#endif

using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

template <typename T>
int disc(T* a, int n)
{
    return unique(a + 1, a + n + 1) - (a + 1);
}

template <typename T>
T lowBit(T x)
{
    return x & -x;
}

template <typename T>
T Rand(T l, T r)
{
    static mt19937 Rand(time(nullptr));
    uniform_int_distribution<T> dis(l, r);
    return dis(Rand);
}

template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
    return (a % b + b) % b;
}

template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
    a %= c;
    T1 ans = 1;
    for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
    return modt(ans, c);
}

template <typename T>
void read(T& x)
{
    x = 0;
    T sign = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')sign = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = (x << 3) + (x << 1) + (ch ^ 48);
        ch = getchar();
    }
    x *= sign;
}

template <typename T, typename... U>
void read(T& x, U&... y)
{
    read(x);
    read(y...);
}

template <typename T>
void write(T x)
{
    if (typeid(x) == typeid(char))return;
    if (x < 0)x = -x, putchar('-');
    if (x > 9)write(x / 10);
    putchar(x % 10 ^ 48);
}

template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
    write(x), putchar(c);
    write(c, y...);
}

template <typename T11, typename T22, typename T33>
struct T3
{
    T11 one;
    T22 tow;
    T33 three;

    bool operator<(const T3 other) const
    {
        if (one == other.one)
        {
            if (tow == other.tow)return three < other.three;
            return tow < other.tow;
        }
        return one < other.one;
    }

    T3() { one = tow = three = 0; }

    T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
    {
    }
};

template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
    if (x < y)x = y;
}

template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
    if (x > y)x = y;
}

constexpr int N = 1e5 + 10;

struct Node
{
    int left, right, cnt;
} node[N << 5];

#define left(x) node[x].left
#define right(x) node[x].right
#define cnt(x) node[x].cnt
int cnt;
int root[N];

int n, k, q;

inline void add(const int pre, int& curr, const int pos, const int l = 0, const int r = n)
{
    node[curr = ++cnt] = node[pre];
    cnt(curr)++;
    const int mid = l + r >> 1;
    if (l == r)return;
    if (pos <= mid)add(left(pre),left(curr), pos, l, mid);
    else add(right(pre),right(curr), pos, mid + 1, r);
}

//查找<=pos的pre数量
inline int query(const int Lnode, const int Rnode, const int pos, const int l = 0, const int r = n)
{
    const int mid = l + r >> 1;
    if (l == r)return cnt(Rnode) - cnt(Lnode);
    const int sum = cnt(left(Rnode)) - cnt(left(Lnode));
    if (pos <= mid)return query(left(Lnode),left(Rnode), pos, l, mid);
    return sum + query(right(Lnode),right(Rnode), pos, mid + 1, r);
}

vector<int> val[N];
int x, last;

inline void solve()
{
    cin >> n >> k;
    forn(i, 1, n)
    {
        cin >> x;
        val[x].push_back(i);
        const int pre = val[x].size() > k ? val[x][val[x].size() - k - 1] : 0; //找pre_k
        add(root[i - 1], root[i], pre); //建主席树计数pre
    }
    cin >> q;
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        l = (l + last) % n + 1, r = (r + last) % n + 1;
        if (l > r)swap(l, r);
        cout << (last = query(root[l - 1], root[r], l - 1)) << endl;
    }
}

signed int main()
{
    // MyFile
    Spider
    //------------------------------------------------------
    // clock_t start = clock();
    int test = 1;
    //    read(test);
    // cin >> test;
    forn(i, 1, test)solve();
    //    while (cin >> n, n)solve();
    //    while (cin >> test)solve();
    // clock_t end = clock();
    // cerr << "time = " << double(end - start) / CLOCKS_PER_SEC << "s" << endl;
}

\[时间复杂度为:\ O((n+q)\log{n})
\]