优化算法之梯度下降|Matlab实现梯度下降算法
题目要求:
使用Matab实现梯度下降法
对于函数:
min
f
(
x
)
=
2
x
1
2
+
4
x
2
2
−
6
x
1
−
2
x
1
x
2
\min f(x)=2 x_{1}^{2}+4 x_{2}^{2}-6 x_{1}-2 x_{1} x_{2}
minf(x)=2x12+4x22−6x1−2x1x2
试采用 MATLAB实现最速下降法求解该问题, 给出具体的迭代过程、 最终优化结果、涉及的代码, 以及自己的心得体会。
摘要
文章主要通过实现grad()函数进行梯度运算。
主要实现的功能:
- 通过Matlab语言实现梯度下降算法
- 利用Matlab的
plot3描绘出梯度下降循环迭代的过程,同时也描绘出极小值随迭代次数的图像。
梯度下降原理
梯度的概念
梯度:是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值。
有大小:变化率最大(为该梯度的模);
有方向:函数在该点处沿着该方向(此梯度的方向)变化最快
定义:
设
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y)在点
P
0
(
x
0
,
y
0
)
P_{0}\left(x_{0}, y_{0}\right)
P0(x0,y0)处存在偏导数
f
x
′
(
x
0
,
y
0
)
f_{x}^{\prime}\left(x_{0}, y_{0}\right)
fx′(x0,y0)和
f
y
′
(
x
0
,
y
0
)
f_{y}^{\prime}\left(x_{0}, y_{0}\right)
fy′(x0,y0),则称向量
{
f
x
′
(
x
0
,
y
0
)
,
f
y
′
(
x
0
,
y
0
)
}
\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\}
{fx′(x0,y0),fy′(x0,y0)}为
f
(
x
,
y
)
在
P
0
(
x
0
,
y
0
)
f(x, y) \text { 在 } P_{0}\left(x_{0}, y_{0}\right)
f(x,y) 在 P0(x0,y0)的梯度,记作:
∇
f
∣
P
0
,
∇
z
∣
P
0
,
gradf
∣
P
0
或
gradz
∣
P
0
\left.\nabla f\right|_{P_{0}},\left.\nabla z\right|_{P_{0}},\left.\operatorname{gradf}\right|_{P_{0}} 或 \left.\operatorname{gradz}\right|_{P_{0}}
∇f∣P0,∇z∣P0,gradf∣P0或gradz∣P0
∴
∇
f
∣
P
0
=
gradf
∣
P
0
=
{
f
x
′
(
x
0
,
y
0
)
,
f
y
′
(
x
0
,
y
0
)
}
\left.\therefore \nabla f\right|_{P_{0}}=\left.\operatorname{gradf}\right|_{P_{0}}=\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\}
∴∇f∣P0=gradf∣P0={fx′(x0,y0),fy′(x0,y0)}
其中:
∇
\nabla
∇(Nabla)算子:
∇
=
∂
∂
x
i
+
∂
∂
y
j
\nabla=\frac{\partial}{\partial x} i+\frac{\partial}{\partial y} j
∇=∂x∂i+∂y∂j
梯度函数:
梯度的大小:
∣
∇
f
∣
=
[
f
x
′
(
x
,
y
)
]
2
+
[
f
y
′
(
x
,
y
)
]
2
|\nabla f|=\sqrt{\left[f_{x}^{\prime}(x, y)\right]^{2}+\left[f_{y}^{\prime}(x, y)\right]^{2}}
∣∇f∣=[fx′(x,y)]2+[fy′(x,y)]2
梯度的方向:
设:
v
=
{
v
1
,
v
2
}
(
∣
v
∣
=
1
)
v=\left\{v_{1}, v_{2}\right\}(|v|=1)
v={v1,v2}(∣v∣=1)是任一给定方向,则对
∇
f
\nabla f
∇f与
v
v
v的夹角
θ
\theta
θ有:
∂
f
∂
v
∣
P
0
=
f
x
′
(
x
0
,
y
0
)
v
1
+
f
y
′
(
x
0
,
y
0
)
v
2
=
{
f
x
′
(
x
0
,
y
0
)
,
f
y
′
(
x
0
,
y
0
)
}
∙
{
v
1
,
v
2
}
=
∇
f
∣
P
0
∙
v
=
∣
∇
f
∣
P
0
∣
⋅
∣
v
∣
cos
θ
\begin{aligned} \left.\frac{\partial f}{\partial v}\right|_{P_{0}} &=f_{x}^{\prime}\left(x_{0}, y_{0}\right) v_{1}+f_{y}^{\prime}\left(x_{0}, y_{0}\right) v_{2} \\ &=\left\{f_{x}^{\prime}\left(x_{0}, y_{0}\right), f_{y}^{\prime}\left(x_{0}, y_{0}\right)\right\} \bullet\left\{v_{1}, v_{2}\right\} \\ &=\left.\nabla f\right|_{P_{0}} \bullet v=|\nabla f|_{P_{0}}|\cdot| v \mid \cos \theta \end{aligned}
∂v∂f
P0=fx′(x0,y0)v1+fy′(x0,y0)v2={fx′(x0,y0),fy′(x0,y0)}∙{v1,v2}=∇f∣P0∙v=∣∇f∣P0∣⋅∣v∣cosθ
梯度下降法:
α
(
k
)
=
argmin
f
(
x
k
−
α
⋅
∇
f
(
x
(
k
)
)
)
\alpha_{(k)}=\operatorname{argmin} f\left(x^{k}-\alpha \cdot \nabla f\left(x^{(k)}\right)\right)
α(k)=argminf(xk−α⋅∇f(x(k)))
梯度下降法的优缺点分析
优点:
(1)程序简单,计算量小;
(2)对初始点没有特别的要求;
(3)最速下降法是整体收敛的,且为线性收敛
缺点:
(1)它只在局部范围内具有“最速”属性, 对整体求解过程,它的下降速度是缓慢的;
(2)靠近极小值时速度减慢;
(3)可能会’之字型’地下降
核心代码和结果
代码的迭代结果:
迭代过程:

极小值-迭代次数趋势图像:
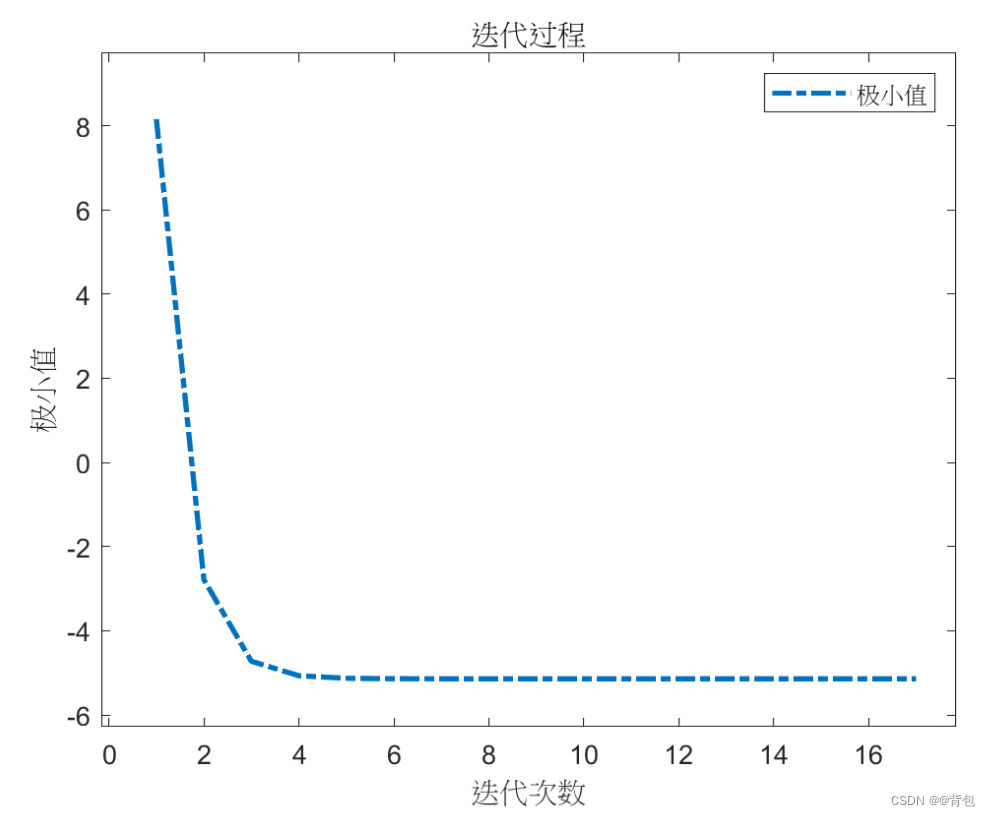
迭代结果在圆锥曲面上的可视化:
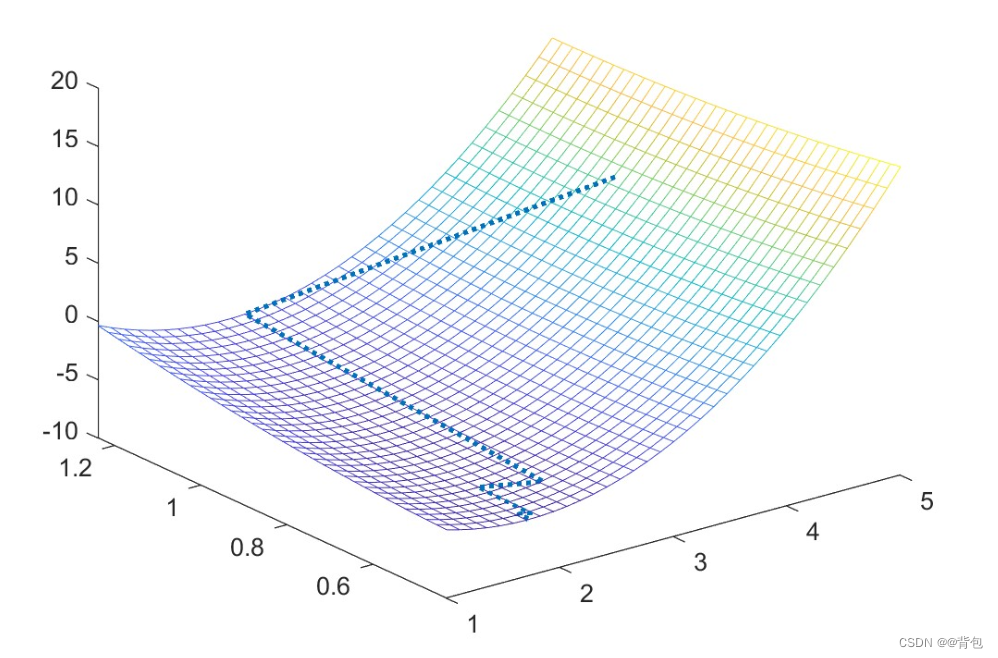
所求函数:
min
f
(
x
)
=
2
x
1
2
+
4
x
2
2
−
6
x
1
−
2
x
1
x
2
\min f(x)=2 x_{1}^{2}+4 x_{2}^{2}-6 x_{1}-2 x_{1} x_{2}
minf(x)=2x12+4x22−6x1−2x1x2
主函数:
clc,clear;
syms x1 x2 s; %声明符号变量
f1 =2*x1^2+4*x2^2-6*x1-2*x1*x2;%设定目标函数
[k,f1,f2,f3]=grad(f1,x1,x2,s,[0,1],10^(-5)); %设定起始点[x1 x2]=[-2.5,4.25]和精度10^(-2)
[result]=sprintf('在 %d 次迭代后求出极小值\n',k);%在迭代多少次之后求出极小值
disp(result);
figure(1);
plot(1:k,f3); % 作出函数图像
title('迭代过程');%输出结果
xlabel('迭代次数');
ylabel('极小值');
figure(2);
plot3(f1,f2,f3); % 画出方程图像
hold on;
syms x1 x2; % 声明符号变量
f=2*x1^2+4*x2^2-6*x1-2*x1*x2;
fmesh(f);
梯度下降核心函数实现:
function [iterator,f1,f2,f3] = grad(f,x1,x2,s,start_point,thereshold)
iterator = 0;%迭代次数赋值初始化
grad_f = [diff(f,x1) diff(f,x2)]; %计算f的梯度
delta = subs(grad_f,[x1,x2],[start_point(1),start_point(2)]);
%计算起点的梯度
step=1; %设置初始步长为1
current_point = start_point;%起点值赋给当前点
%最速下降法的主循环,判断条件为:梯度的模与所给精度值进行比较
while norm(delta) > thereshold
iterator = iterator + 1;%迭代次数+1
%一维探索 求最优步长(此时方向已知,步长s为变量)
x_next = [current_point(1),current_point(2)] - s* delta/norm(delta);% 计算x(k+1)点,其中步长s为变量
f_val = subs(f,[x1,x2],[x_next(1),x_next(2)]);% 将x值带入目标函数中
step = abs(double(solve(diff(f_val,s)))); % 对s求一阶导,并加绝对值符号,得到最优步长的绝对值
step = step(1);%更新步长
%计算x(k+1)点
current_point = double([current_point(1),current_point(2)] - step * delta/norm(delta));
%计算x(k+1)点的梯度值
delta = subs(grad_f,[x1,x2],[current_point(1),current_point(2)]);
%计算函数值
f_value = double(subs(f,[x1,x2],[current_point(1),current_point(2)]));
%输出迭代计算过程
result_string=sprintf('k=%d, x1=%.6f, x2=%.6f, step=%.6f f(x1,x2)=%.6f',iterator,current_point(1),current_point(2),step,f_value);
f1(iterator)=current_point(1);
f2(iterator)=current_point(2);
f3(iterator)=f_value;
disp(result_string);
end
end
梯度算法的局限性及其优化
神经网络中,梯度的搜索是使用最为广泛的参数寻优方法,在此类方法美些视策解出发,代寻找最优参数值、每次送代中,我们先计算设置函数当前点的梯度,并根据梯度确定搜索方向。
在搜索过程中,我们可能会遇到陷入局部最小的问题,如果误差函数具有多个局部极小,则不能保证找到的解是全局最小,对后一种情形,我们称参数寻优陷入了局部极小,这显然不是我们所希望的。
在现实任务中,人们常采用以下策略来试图“跳出”局部极小 从而进-步接近全局最小:
- 以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数.这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小,从中进行选择有可能获得更接近全局最小的结果.
但是也会造成“跳出”全局最小 - 使用“模拟退火”技术,模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助于“跳出”局部极小.在每步迭代过程中、接受“你优解》的概率要随着时间的摊移而逐渐降低。从而保证算法稳定
- 使用随机梯度下降.与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素。于是,即便陷入局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索。
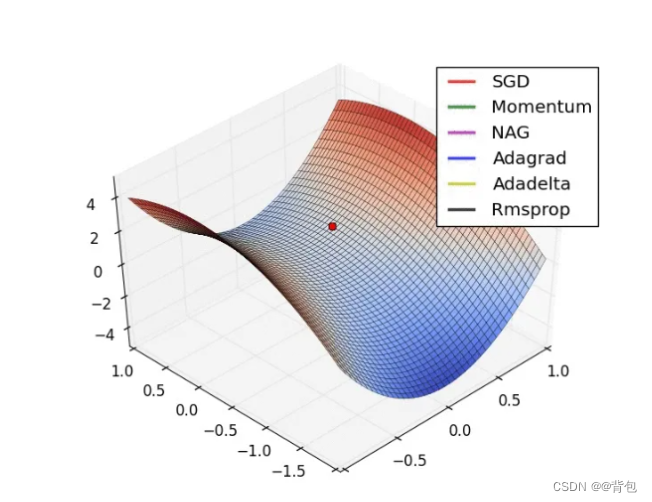
优化算法之梯度下降|Matlab实现梯度下降算法的更多相关文章
- NN优化方法对照:梯度下降、随机梯度下降和批量梯度下降
1.前言 这几种方法呢都是在求最优解中常常出现的方法,主要是应用迭代的思想来逼近.在梯度下降算法中.都是环绕下面这个式子展开: 当中在上面的式子中hθ(x)代表.输入为x的时候的其当时θ參数下的输出值 ...
- 机器学习(ML)十五之梯度下降和随机梯度下降
梯度下降和随机梯度下降 梯度下降在深度学习中很少被直接使用,但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础.随后,将引出随机梯度下降(stochastic ...
- 梯度下降、随机梯度下降、方差减小的梯度下降(matlab实现)
梯度下降代码: function [ theta, J_history ] = GradinentDecent( X, y, theta, alpha, num_iter ) m = length(y ...
- 梯度下降之随机梯度下降 -minibatch 与并行化方法
问题的引入: 考虑一个典型的有监督机器学习问题,给定m个训练样本S={x(i),y(i)},通过经验风险最小化来得到一组权值w,则现在对于整个训练集待优化目标函数为: 其中为单个训练样本(x(i),y ...
- 机器学习笔记 1 LMS和梯度下降(批梯度下降) 20170617
https://www.cnblogs.com/alexYuin/p/7039234.html # 概念 LMS(least mean square):(最小均方法)通过最小化均方误差来求最佳参数的方 ...
- L20 梯度下降、随机梯度下降和小批量梯度下降
airfoil4755 下载 链接:https://pan.baidu.com/s/1YEtNjJ0_G9eeH6A6vHXhnA 提取码:dwjq 梯度下降 (Boyd & Vandenbe ...
- 梯度下降VS随机梯度下降
样本个数m,x为n维向量.h_theta(x) = theta^t * x梯度下降需要把m个样本全部带入计算,迭代一次计算量为m*n^2 随机梯度下降每次只使用一个样本,迭代一次计算量为n^2,当m很 ...
- online learning,batch learning&批量梯度下降,随机梯度下降
以上几个概念之前没有完全弄清其含义及区别,容易混淆概念,在本文浅析一下: 一.online learning vs batch learning online learning强调的是学习是实时的,流 ...
- 梯度下降取负梯度的简单证明,挺有意思的mark一下
本文转载自:http://blog.csdn.net/itplus/article/details/9337515
- 深度学习必备:随机梯度下降(SGD)优化算法及可视化
补充在前:实际上在我使用LSTM为流量基线建模时候,发现有效的激活函数是elu.relu.linear.prelu.leaky_relu.softplus,对应的梯度算法是adam.mom.rmspr ...
随机推荐
- Codeforce 318A - Even Odds(数学水题)
Being a nonconformist, Volodya is displeased with the current state of things, particularly with the ...
- Educational Codeforces Round 94 (A - D题题解)
https://codeforces.com/contest/1400/problem/A Example input 4 1 1 3 00000 4 1110000 2 101 output 1 0 ...
- 启动vue项目失败,报错Failed at the node-sass@4.14.1 postinstall script.
https://www.cnblogs.com/xiaodangshan/p/13061618.html
- shell脚本(13)-shell函数
一.函数介绍 将相同功能的代码模块化,使得代码逻辑上比较简单,代码量少,排错容易 函数的优点: 1.代码模块化,调用方便,节省内存 2.代码模块化,代码量少,排错简单 3.代码模块化,可以改变代码的执 ...
- Liunx常用操作(七)-文件上传下载方法
如下介绍了几个比较方便的liunx软件的文件维护方法 一.SZ,RZ liunx服务器上安装 通过apt来安装z.sz:安装后直接上传下载文件 apt-get install lrzsz 用法: # ...
- Spring Boot 中使用Caffeine缓存的简单例子
Caffeine 缓存是 Java 的高性能缓存库.本文简单记录下 Caffeine 缓存的用法. 依赖配置 <dependencies> <dependency> <g ...
- IDE-常用插件
2021-8-25_IDE-常用插件 1. 背景 提升编写代码的舒适度,提升开发效率 2. 常用插件列表 IDE EVal Reset 白嫖付费的golang编辑器,reset插件可以重置golang ...
- [转帖]goofys
Goofys is a high-performance, POSIX-ish Amazon S3 file system written in Go Overview Goofys all ...
- [转帖]ChatGPT研究框架(2023)
https://www.eet-china.com/mp/a226595.html ChatGPT是基于OpenAI公司开发的InstructGPT模型的对话系统,GPT系列模型源自2017年诞生的T ...
- [转帖]36.堆空间的参数设置和-XX:HandlePromotionFailure
目录 1.堆空间参数 2.-XX:HandlePromotionFailure 1.堆空间参数 * -XX:+PrintFlagsInitial : 查看所有的参数的默认初始值 * -XX:+Prin ...
