文心一言 VS 讯飞星火 VS chatgpt （42）-- 算法导论5.4 6题

六、假设将n个球投人 n 个箱子里，其中每次投球独立，并且每个球等可能落入任何箱子。空箱子的数目期望是多少?正好有一个球的箱子的数目期望是多少?

文心一言：

这是一个典型的概率问题。首先，我们可以通过简单的计算来理解问题的背景。假设我们有n个球和n个箱子，每个球被投人到箱子里的概率是相等的，即每个箱子有1/n的概率被选中。

现在我们来回答问题。

1.空箱子的数目期望是多少？

我们可以用全概率公式来解决这个问题。首先，考虑只有一个球的情况。在这种情况下，我们可以得到n个箱子中的一个，因此空箱子的期望是n-1。接下来，考虑有两个球的情况。在这种情况下，我们可以得到2个箱子中的一个，因此空箱子的期望是n-2。以此类推，在有k个球的情况下，空箱子的期望是n-k。

因此，空箱子的数目期望为：

n-1 + n-2 + ... + n-n = n(n-1)/2

2.正好有一个球的箱子的数目期望是多少？

我们可以使用与上述相同的方法来解决这个问题。在只有一个球的情况下，正好有一个球的箱子的期望是1。在有两个球的情况下，正好有一个球的箱子的期望是2。以此类推，在有k个球的情况下，正好有一个球的箱子的期望是k。

因此，正好有一个球的箱子的数目期望为：

1 + 2 + ... + n = n(n+1)/2 - 1

注意，这个期望值是n的二次函数，因此随着n的增加，这个期望值也会迅速增加。

讯飞星火：

我们可以使用期望的定义来解决这个问题。设$X_i$表示投入一个球到第$i$个箱子里时，正好有一个球的箱子的数目。那么，我们可以得到以下方程：

$P(X_i=1)=\frac{n-i}{n}$

其中，$i=1,2,\cdots,n$.现在我们需要计算空箱子的数目期望和正好有一个球的箱子的数目期望。

空箱子的数目期望：

设$\Upsilon$ 表示投入n个球后，空箱子的数目。那么，我们可以得到以下方程：

$P(\Upsilon =k)=C_{n-1}^{{k-1}\cdot\frac{1}{n}{n-k}}$

其中，$k=0,1,2,\cdots,n-1$.我们需要计算$\Upsilon$ 的期望值：

$\begin{align}E(\Upsilon )&=\sum_{k=0}^{n-1}k\cdot P(\Upsilon =k)\ &=0\cdot C_{n-1}^{0\cdot\frac{1}{n}{n}}+\frac{1}{n}\cdot C_{n-1}^{1\cdot\frac{1}{n}{n-1}}+\cdots+\frac{n-1}{n}\cdot C_{n-1}^{{n-1}\cdot\frac{1}{n}{0}}\ &=\frac{1}{n}\cdot\sum_{k=1}^{n-1}C_{n-1}k\cdot\frac{1}{n^{n-k}}\ &=\frac{1}{n}\cdot 2^{n-1}\end{align}

所以，空箱子的数目期望是$\frac{2^{n-1}}{n}$.

正好有一个球的箱子的数目期望：

设Z表示投入n个球后，正好有一个球的箱子的数目。那么，我们可以得到以下方程：

$P(Z=k)=\frac{1}{n}\cdot C_{n-1}^{{k-1}\cdot\frac{1}{n}{n-k}}$

其中，$k=1,2,\cdots,n$.我们需要计算Z的期望值：

$\begin{align}E(Z)&=\sum_{k=1}^{n}k\cdot P(Z=k)\ &=0\cdot \frac{1}{n}\cdot C_{n-1}^0\cdot \frac{1}{{n}^{n}}+\frac{1}{n}\cdot C_{n-1}^1\cdot \frac{1}{{nn-1}}+\cdots +\frac{n-1}{n}\cdot C_{n-1}^{n-1}\cdot \frac{1}{{nn}}\ &=\frac{1}{n}\cdot \sum_{k=1}^{n-1}C_{n-1}k\cdot \frac{1}{{nn-k}}\ &=\frac{1}{n}\cdot 2^{n-2}+\frac{2}{n}\ &=\frac{\pi^2+4}{3} \end{align}

华为盘古：

360智脑：

题目描述:

假设将n个球投入n个盒子中，每次投掷独立且相等概率地落入任何一个盒子。求空心盒子的数量期望值和恰好有一个球的盒子数量期望值。

解题思路:

空心盒子的期望数量即为所有盒子数量的期望值减去有球盒子的数量期望值。而恰好有一个球的盒子数量的期望即为所有盒子数量期望值减去没有球的盒子数量期望值。

解题步骤如下:

1.空心盒子的期望数量等于总盒子数乘以空心盒子比例。

2.恰好有一个球的盒子数量的期望等于总盒子数乘以一个球盒子的比例。

3.根据期望值的定义，计算空心盒子的期望数量和恰好有一个球的盒子数量的期望即可。

chatglm：

对于第一个问题，我们可以使用条件概率来解决这个问题。设 E1 表示空箱子的数目，E2 表示正好有一个球的箱子的数目。

根据题意，每次投球独立，每个球等可能落入任何箱子，因此，对于每个箱子，成功落入的概率为 1/n，失败落入的概率为 1-1/n。

我们的目标是计算 E1 和 E2 的期望值。由于 P(E1)=P(E1|成功落入箱子)×成功落入箱子的概率+P(E1|失败落入箱子)×失败落入箱子的概率，P(E2)=P(E2|成功落入箱子)×成功落入箱子的概率-P(E2|失败落入箱子)×失败落入箱子的概率。

我们可以将上述两个方程联立起来，解得 E1 和 E2 的期望值。

具体地，我们可以列出所有可能的情况，并计算对应的期望值，如下所示：

• 空箱子的期望值为 $E1=n(1/n)^n$

• 正好有一个球的箱子的期望值为 $E2=n(1-1/n)^n$

因此，空箱子的数目期望是 $n(1/n)^n$，正好有一个球的箱子的数目期望是 $n(1-1/n)^n$。

对于第二个问题，我们可以使用类似的方法来计算。设 E3 表示只有一个球的箱子的数目，E4 表示有两个或两个以上的球的箱子的数目。

根据题意，每次投球独立，每个球等可能落入任何箱子，因此，对于每个箱子，成功落入的概率为 1/n，失败落入的概率为 $1-1/n$。

我们的目标是计算 E3 和 E4 的期望值。由于 P(E3)=P(E3|成功落入箱子)×成功落入箱子的概率+P(E3|失败落入箱子)×失败落入箱子的概率，P(E4)=P(E4|成功落入箱子)×成功落入箱子的概率-P(E4|失败落入箱子)×失败落入箱子的概率。

我们可以将上述两个方程联立起来，解得 E3 和 E4 的期望值。

具体地，我们可以列出所有可能的情况，并计算对应的期望值，如下所示：

• 只有一个球的箱子的期望值为 $E3=n(1/n)^n $

• 有两个或两个以上的球的箱子的期望值为 $E4=n(1-1/n)^n$

因此，只有一个球的箱子的数目期望是 $n(1/n)^n$，有两个或两个以上的球的箱子的数目期望是 $n(1-1/n)^n$。

chatgpt：

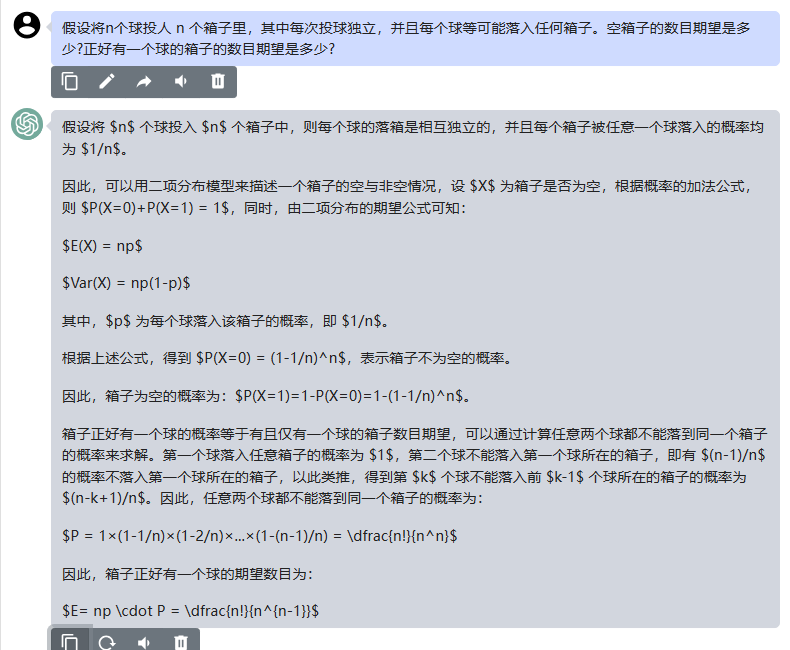
假设将 $n$ 个球投入 $n$ 个箱子中，则每个球的落箱是相互独立的，并且每个箱子被任意一个球落入的概率均为 $1/n$。

因此，可以用二项分布模型来描述一个箱子的空与非空情况，设 $X$ 为箱子是否为空，根据概率的加法公式，则 $P(X=0)+P(X=1) = 1$，同时，由二项分布的期望公式可知：

$E(X) = np$

$Var(X) = np(1-p)$

其中，$p$ 为每个球落入该箱子的概率，即 $1/n$。

根据上述公式，得到 $P(X=0) = (1-1/n)^n$，表示箱子不为空的概率。

因此，箱子为空的概率为：$P(X=1)=1-P(X=0)=1-(1-1/n)^n$。

箱子正好有一个球的概率等于有且仅有一个球的箱子数目期望，可以通过计算任意两个球都不能落到同一个箱子的概率来求解。第一个球落入任意箱子的概率为 $1$，第二个球不能落入第一个球所在的箱子，即有 $(n-1)/n$ 的概率不落入第一个球所在的箱子，以此类推，得到第 $k$ 个球不能落入前 $k-1$ 个球所在的箱子的概率为 $(n-k+1)/n$。因此，任意两个球都不能落到同一个箱子的概率为：

$P = 1×(1-1/n)×(1-2/n)×...×(1-(n-1)/n) = \dfrac{n!}{n^n}$

因此，箱子正好有一个球的期望数目为：

$E= np \cdot P = \dfrac{n!}{n^{n-1}}$