CODE FESTIVAL 2017 qual A D Four Coloring（补题）

这题看了好几天才看懂，一直误解题解中的d * d了

题解中说把大的格子划分成d * d的方格，我划分的时候把格子当作点来算的，一直觉得那明明是(d-1) * (d-1)，昨天刚反映过来

思路：把格子旋转45度，坐标扩大sqrt(2)倍，也就是(i,j) - > (i+j,i-j)，把曼哈顿距离转换为切比雪夫距离来进行计算。旋转前的曼哈顿距离就是旋转后的切比雪夫距离

把旋转后的格子划分成d * d的格子后，小格子内方格之间的距离最大为d-1，一个小格子是一个部分，可以涂成相同颜色而不违反题目要求。

一个d * d的格子有8个邻居的格子，要保证他和这8个格子颜色不同，如果相同了，就不满足题目要求了。

这时候对颜色的选择，可以根据格子的坐标的奇偶性来选择。

假设当前格子是(n,n),n是偶数，则周围的格子是(n+1,n),(n-1,n),(n,n+1),(n,n-1),(n+1,n+1),(n-1,n-1),(n+1,n-1),(n-1,n+1)。

会发现(n,n)左右的格子坐标奇偶性一致，上下的也一致，四个角的格子，奇偶性一致，还有当前格子，正好四部分。

在代码中计算时，(x%2,y%2)之后，得到的是(0,0),(1,1),(0,1),(1,0)四种坐标，对应二进制的0-3，正好对应四种颜色。



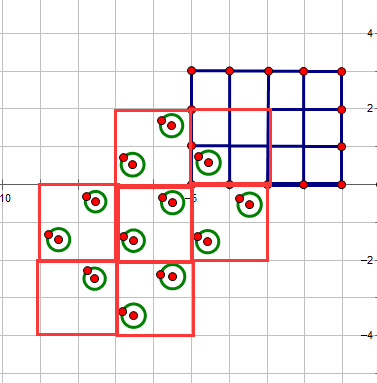
圆圈组成的格子是旋转后的

#include <bits/stdc++.h>
using namespace std;

char color[5] = "RYGB";

int main()
{
    int h,w,d,x,y;
    scanf("%d %d %d",&h,&w,&d);
    for(int i = 1 ;i <= h; ++i)
    {
        for(int j = 1; j <= w; ++j)
        {
            //映射坐标，+500是防止出现负数，都+500是保持俩数的奇偶性不变
            x = (i+j+500)/d;
            y = (i-j+500)/d;
            //根据坐标奇偶性来判断颜色
            putchar(color[(x%2)*2+y%2]);
        }
        putchar('\n');
    }
    return 0;
}