深度优先搜索DFS---求出矩阵中“块”的个数。

题目：

　　给出一个 m x n 的矩阵，矩阵中的元素为0或1。如果矩阵中有若干个 1是相邻的，那么称这些1构成了一个“块”。求给定的矩阵中“块”的个数。

0 1 1 1 0 0

0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 1 1 1 0

1 1 1 0 0 0

1 1 1 1 0 0 0

例如上面的 6 x 7的矩阵中，“块”的个数为4。

输入格式：

第一行给出 m，n（1<=m，n<= 20）分别表示矩阵的行，列。

每一行给出 n个数（0或者1），共m行。

输出格式：

输出矩阵中“块”的个数。

输入样例：

6 7

0 1 1 1 0 0 1

0 0 1 0 0 0 0

0 0 0 0 1 0 0

0 0 0 1 1 1 0

1 1 1 0 1 0 0

1 1 1 1 0 0 0

输出样例：

4

直接上代码。。。

 #include<iostream>
 using namespace std;

 const int maxn = ;
 int matrix[maxn][maxn];
 int m,n,CNT = ;

 void DFS(int i, int j) {
     if(i <  || j <  || i >= m || j>= n || matrix[i][j] == )//不能逾越矩阵边界,或者元素为 0---即递归边界
         return ;
     //右下左上，作为四个选择分支
     matrix[i][j] = ;//访问的元素 1，置为 0
     DFS(i,j+);//右
     DFS(i+,j);//下
     DFS(i,j-);//左
     DFS(i-,j);//上
 }

 int main() {
     cin>>m>>n;
     for(int i = ; i < m; ++i) { //初始化矩阵
         for(int j = ; j < n; ++j)
             cin>>matrix[i][j];
     }
     for(int i = ; i < m; ++i) {//暴力DFS，哈哈哈
         for(int j = ; j < n; ++j) {
             if(matrix[i][j] == ) {
                 DFS(i,j);
                 CNT++;
             }
         }
     }
     cout<<CNT;//输出矩阵中”块“ 的个数
     return ;
 }

运行结果：

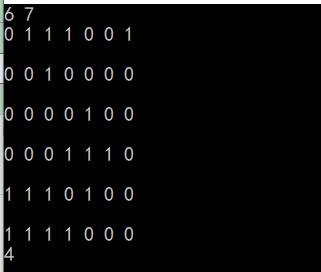
PS：暴力大法好！！！