[CQOI2011]放棋子--DP

题目描述：

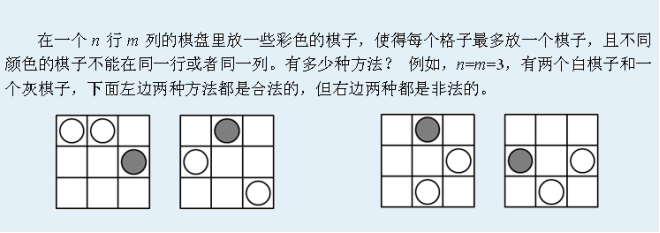
输入格式

输入第一行为两个整数n, m, c，即行数、列数和棋子的颜色数。
第二行包含c个正整数，即每个颜色的棋子数。
所有颜色的棋子总数保证不超过nm。
N,M<=30 C<=10 总棋子数有大于250的情况

输出格式

输出仅一行，即方案总数除以 1,000,000,009的余数。

样例

样例输入

4 2 2
3 1

样例输出

8

数据范围与提示

30% n,m<=10

solution:10%:cout<<0<<endl;

肯定有0的情况比如c>min(n,m)之类的。。。

20%：搜索，枚举所有状态。

据说这是搜索最高得分，然而博主考试时只拿到10分，而且还不是TLE。

---

下面说正解

我们考虑dp，设f[i][j][k]表示前k种颜色的棋子占领任意i行j列的方案数，g[i][j][k]表示第k种颜色的所有棋子占领任意i行j列的方案数;

那么我们首先可以得到g[i][j][k]=$C_{i*j}^{num[k]}$-$\sum_\limits{p=1}^{i}$$\sum_\limits{q=1}^{j}$g[p][q][k]*$C_{i}^{p}$*$C_{j}^{q}$

其实就是用合法的减去不合法的（实际上有没有被占领的行或列的方案数）

接下来得到f的方程：

$f[i][j][k]=\sum_{p=0}^{i-1}\sum_{q=0}^{j-1}$

$f[i][j][k]=\sum_{p=0}^{i-1}\sum_{q=0}^{j-1}f[p][q][k-1]*g[i-p][j-q][k]*C_{n-p}^{i-p}*C_{m-q}^{j-q}$，f[0][0][0]=1;

p，q，k-1就是枚举的上一个状态，$C_{n-p}^{i-p}$表示n-p行中选出i-p行放棋子，$C_{m-q}^{i-q}$同理，

最后ans=$\sum_{i=1}^{n}$$\sum_{j=1}^{m}$f[i][j][c]，于是这道题就完美地解决了

放代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define mod 1000000009
 #define ll long long
 #define MAXNM 905
 using namespace std;
 int n,m,c,num[];
 ll C[MAXNM][MAXNM],g[][][],f[][][],ans=;
 int main(){
     scanf("%d%d%d",&n,&m,&c);
     for(int i=;i<=n*m;i++){
         C[i][]=;
         for(int j=;j<=i;j++)
             C[i][j]=(C[i-][j]+C[i-][j-])%mod;
     }
     f[][][]=;
     for(int k=;k<=c;k++)
         scanf("%d",&num[k]);
     for(int k=;k<=c;k++){
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++){
                 if(i*j<num[k]) continue;
                 g[i][j][k]=C[i*j][num[k]];
                 for(int p=;p<=i;p++)
                     for(int q=;q<=j;q++){
                         if(p<i||q<j)
                             g[i][j][k]=(g[i][j][k]-g[p][q][k]*C[i][p]%mod*C[j][q]%mod)%mod;
                         //cout<<g[i][j]<<endl;
                     }
             }
     }
     for(int k=;k<=c;k++){
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++)
                 for(int p=;p<i;p++)
                     for(int q=;q<j;q++){
                         int l=i-p,r=j-q;
                         if(l*r<num[k]) continue;
                         f[i][j][k]=(f[i][j][k]+f[p][q][k-]*g[l][r][k]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod;
                         //cout<<f[i][j][k]<<endl;
                     }
     }
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             ans=(ans+f[i][j][c])%mod;
     printf("%lld\n",ans);
     return ;
 }

我们发现g只对当前一种棋子有贡献，所以第三维可以干掉，在每次输入时处理g和f

#include<iostream>
#include<cstdio>
#include<cstring>
#define mod 1000000009
#define ll long long
#define MAXNM 905
using namespace std;
int n,m,c,num[12];
ll C[MAXNM][MAXNM],g[35][35],f[35][35][15],ans=0;
int main(){
	scanf("%d%d%d",&n,&m,&c);
	for(int i=0;i<=n*m;i++){
		C[i][0]=1;
		for(int j=1;j<=i;j++)
			C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
	}
	f[0][0][0]=1;
	for(int k=1;k<=c;k++){
		scanf("%d",&num[k]);
		memset(g,0,sizeof(g));
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++){
				if(i*j<num[k]) continue;
				g[i][j]=C[i*j][num[k]];
				for(int p=1;p<=i;p++)
					for(int q=1;q<=j;q++){
						if(p<i||q<j)
							g[i][j]=(g[i][j]-g[p][q]*C[i][p]%mod*C[j][q]%mod)%mod;
						//cout<<g[i][j]<<endl;
					}
			}
		for(int i=1;i<=n;i++)
		　　　　for(int j=1;j<=m;j++)
				for(int p=0;p<i;p++)
					for(int q=0;q<j;q++){
						int l=i-p,r=j-q;
						if(l*r<num[k]) continue;
						f[i][j][k]=(f[i][j][k]+f[p][q][k-1]*g[l][r]%mod*C[n-p][l]%mod*C[m-q][r]%mod)%mod;
						//cout<<f[i][j][k]<<endl;
					}
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			ans=(ans+f[i][j][c])%mod;
	printf("%lld\n",ans);
	return 0;
}