@NOIP2018 - D2T2@ 填数游戏

目录

• @题目描述@
• @题解@
• @代码@

---

@题目描述@

小 D 特别喜欢玩游戏。这一天，他在玩一款填数游戏。

这个填数游戏的棋盘是一个 n×m 的矩形表格。玩家需要在表格的每个格子中填入一个数字（数字 0 或者数字 1 ），填数时需要满足一些限制。

下面我们来具体描述这些限制。

为了方便描述，我们先给出一些定义：

我们用每个格子的行列坐标来表示一个格子，即（行坐标，列坐标）。（注意： 行列坐标均从 0 开始编号）

一条路径是合法的当且仅当：

（1）这条路径从矩形表格的左上角的格子(0,0)出发，到矩形的右下角格子 (n−1,m−1)结束；

（2）在这条路径中，每次只能从当前的格子移动到右边与它相邻的格子，或者 从当前格子移动到下面与它相邻的格子。

对于一条合法的路径 P，我们可以用一个字符串 w(P) 来表示，该字符串的长度为 n+m−2，其中只包含字符“R”或者字符“D”， 第 i 个字符记录了路径 P 中第 i 步的移动 方法，“ R”表示移动到当前格子右边与它相邻的格子，“ D”表示移动到当前格子下面 与它相邻的格子。

同时，将每条合法路径 P 经过的每个格子上填入的数字依次连接后，会得到一个长 度为 n+m−1 的 01 字符串，记为 s(P) 。

游戏要求小 D 找到一种填数字 0、 1 的方法，使得对于两条路径P1，P2，如果w(P1) > w(P2)，那么必须s(P1) ≤ s(P2)。

但是仅仅是找一种方法无法满 足小 D 的好奇心，小 D 更想知道这个游戏有多少种玩法，也就是说，有多少种填数字 的方法满足游戏的要求？

小 D 能力有限，希望你帮助他解决这个问题，即有多少种填 0、1 的方法能满足题目要求。由于答案可能很大，你需要输出答案对 10^9 + 7 取模的结果。

输入

输入共一行，包含两个正整数 n,m，由一个空格分隔，表示矩形的大小。其中 n 表示矩形表格的行数，m 表示矩形表格的列数。

输出

输出共一行，包含一个正整数，表示有多少种填 0、1 的方法能满足游戏的要求。 注意：输出答案对 10^9+7 取模的结果。

输入样例#1

2 2

输出样例#1

12

输入样例#2

3 3

输出样例#2

112

输入样例#3

5 5

输出样例#3

7136

数据规模与约定

n<=8，m<=10^6。

@题解@

傻逼规律题，我竟然不会做。

我太弱了……

题目中的限制等价于：对于所有的点，如图示的红色路径的数字串要 ≥ 蓝色路径的数字串。

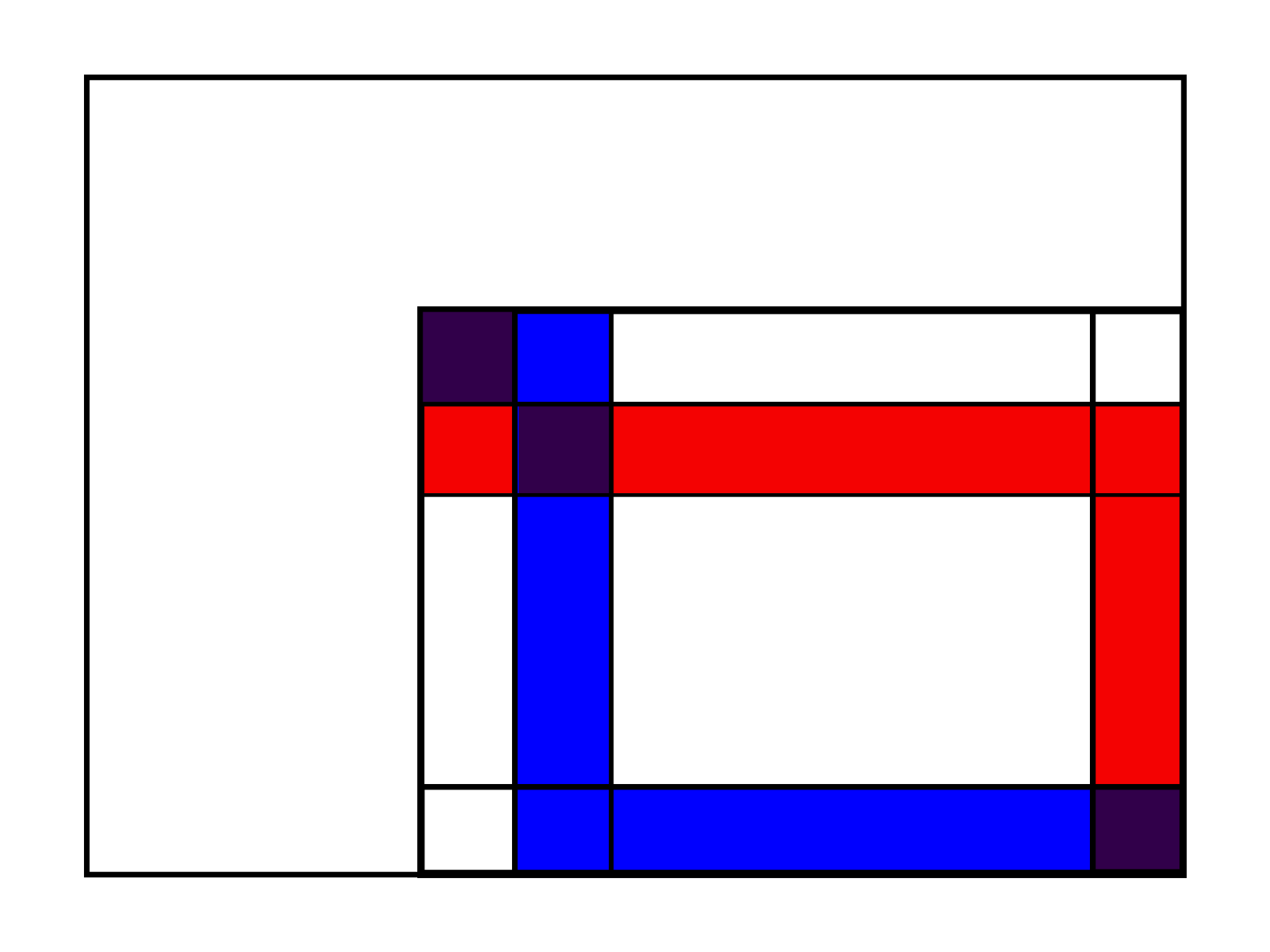
我们再把这个限制进行转换：

（1）每一条自右上至左下的对角线的数字总是先出现一堆 0，再出现一堆 1。

（2）如果 (a, b+1) = (a+1, b)，则以(a+1, b+1)为左上角，以(n-1, m-1)为右下角的矩形，每一条自右上至左下的对角线的数字全部相同。

可以证明以上的转换都是等价的。

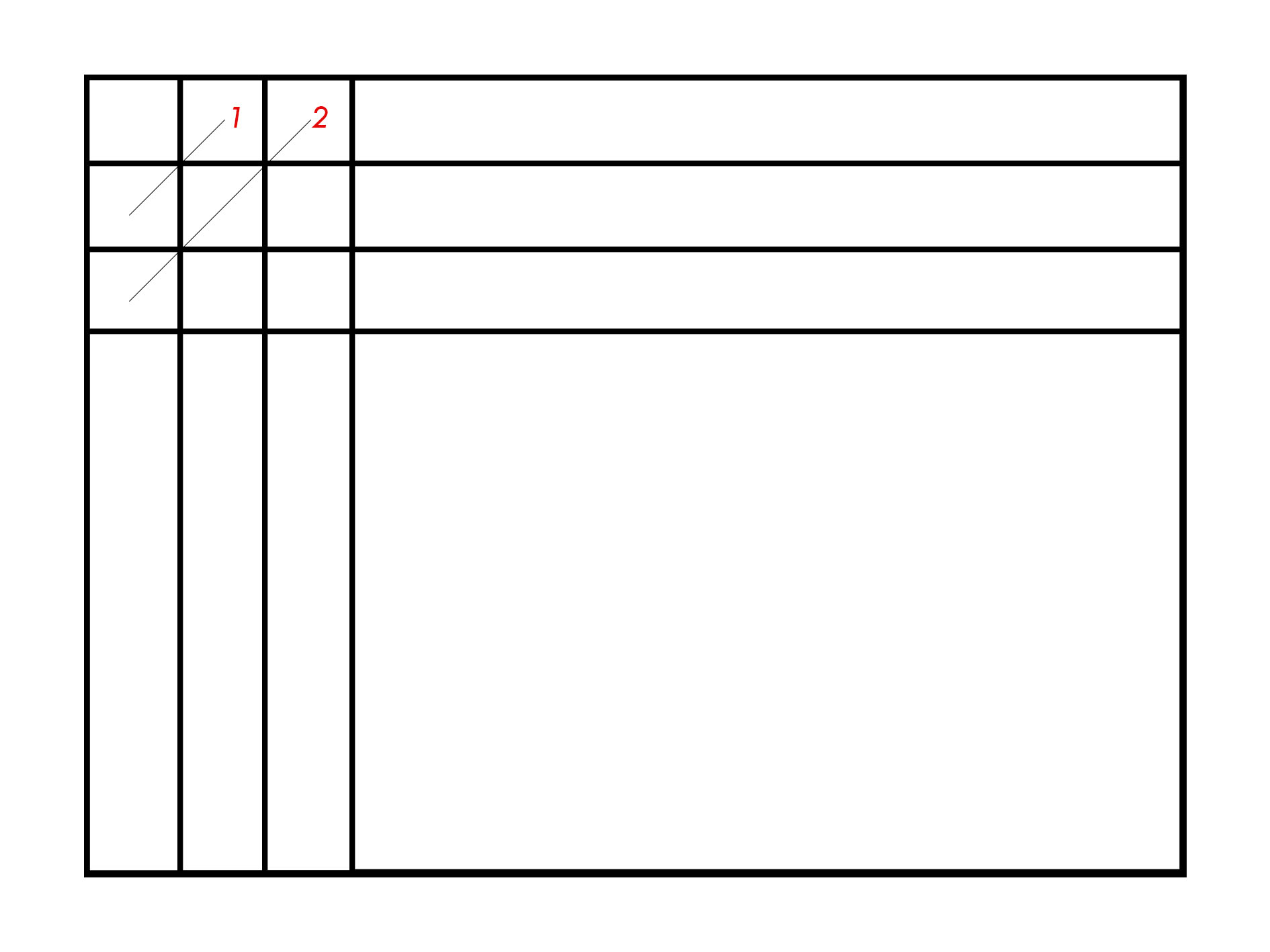
然后就会发现一件很有意思的事情：对于这条对角线 2，肯定是000,001,011,111。这条对角线上一定有 2 个元素相同，也就说限制（2）会限制掉很大一个区域！

于是我们就可以根据这个设计算法了：

先手推 n = 1，n = 2， n = 3 的情况，将它们特判掉。

当 n = 1 时，ans = 2^m。

当 n = 2 时，ans = 4*3^m-1。

当 n = 3 时，ans = 112*3^m-3。

然后：如果交换 n 和 m ，答案不会变。所以我们不妨假设 n <= m。

计算出上图中对角线 1 为 00, 11 的方案数。除此之外对角线 1 一定为 01。

对于对角线 2，先考虑它为 000,111 的情况，然后考虑它为 001,011 的情况。

接下来考虑如何具体计数。

假如对角线 1 为 00, 11：



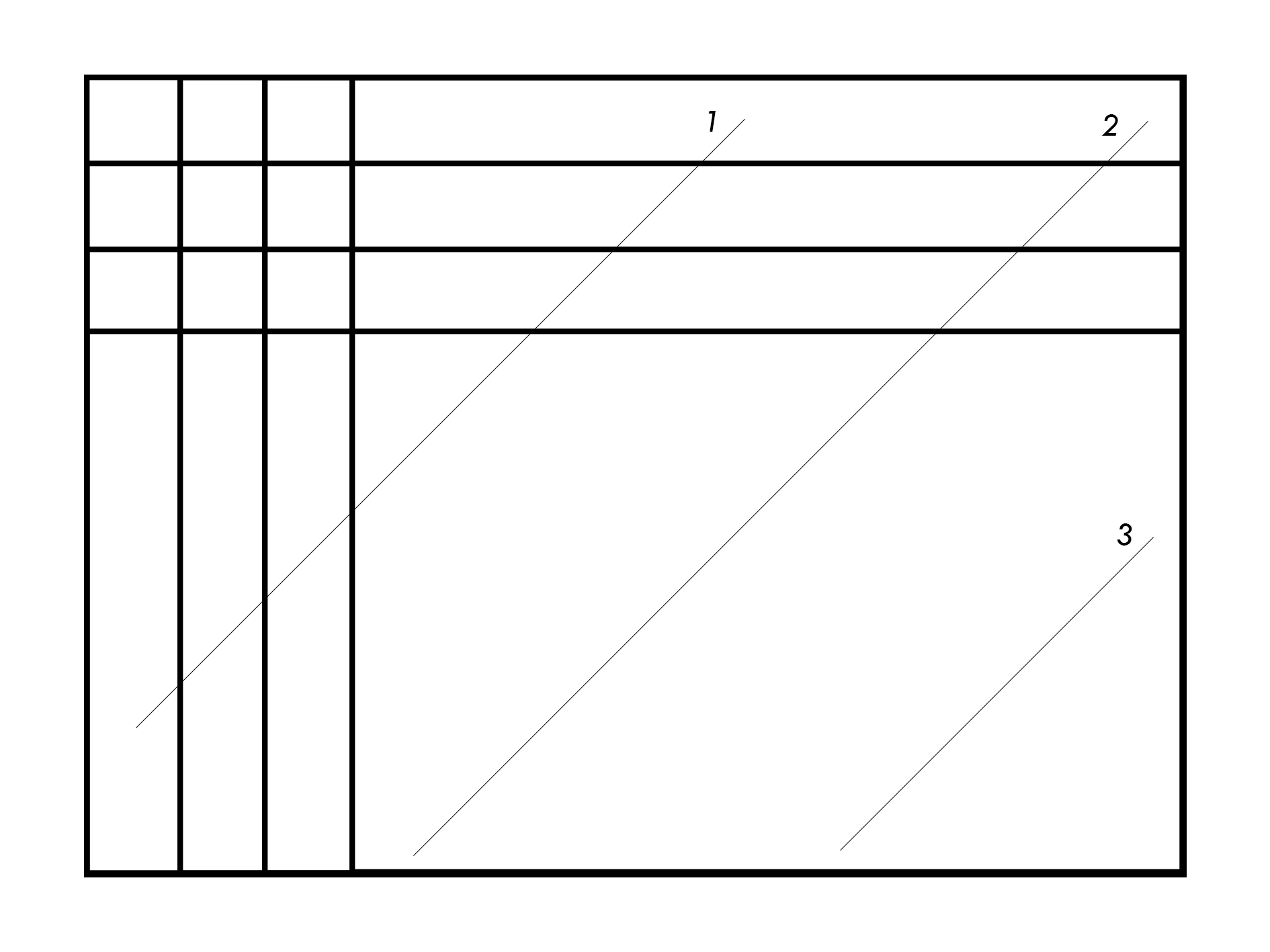
将剩余的对角线分为三类：两个端点没有被限制（形如 1），对答案的贡献为 4；两个端点被限制了一个（形如 2），对答案的贡献为 3；两个端点都被限制（形如 3），对答案的贡献为 2。将所有对角线的贡献乘起来即可。可以用快速幂。

假如对角线 2 为 000, 111：



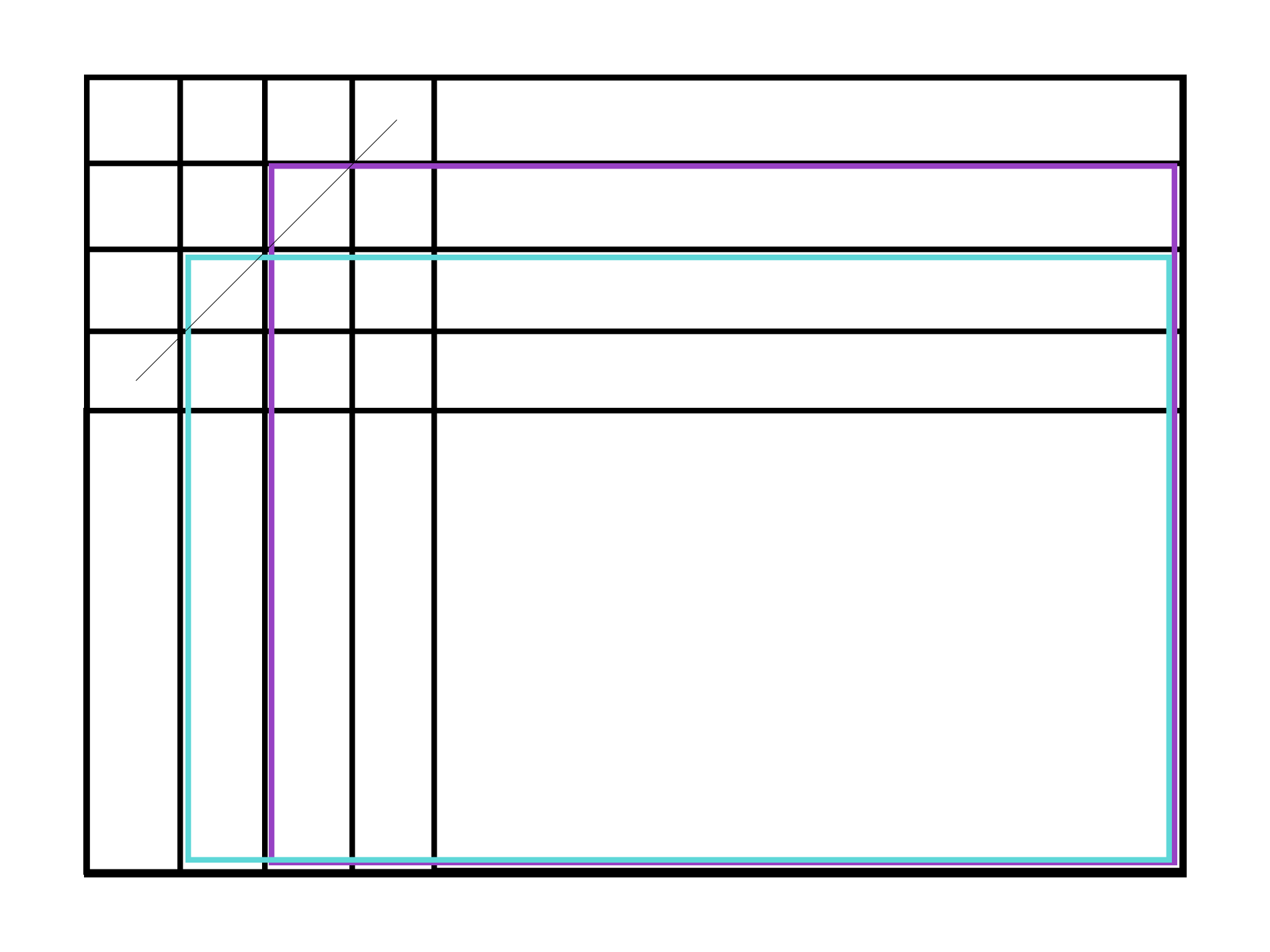
图中所标出的对角线是不受限制的。蓝色限制与紫色限制相互组合，可以发现和上面那种情况是差不大多的（除了边缘的行列都被限制）。因此，依然还是按照上文所提到的方法进行计数。

假如对角线 2 为 001,011。因为是对称的，我们只需要弄清 001 的求解方式即可类比推导出 011 的求解方法。



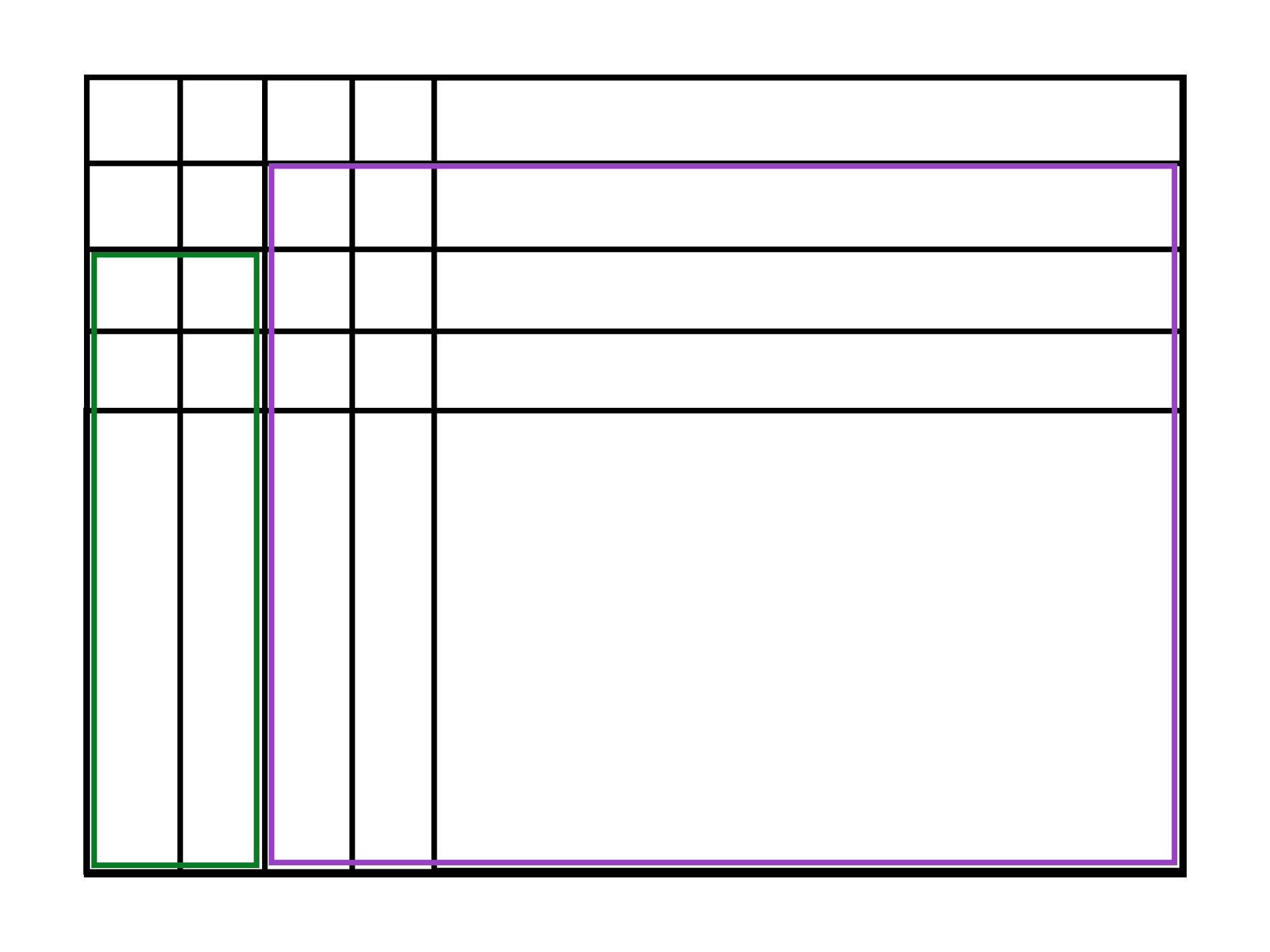
紫色是限制区域。如果绿色矩形中有一个对角线相同，则限制区域会如下图所示。



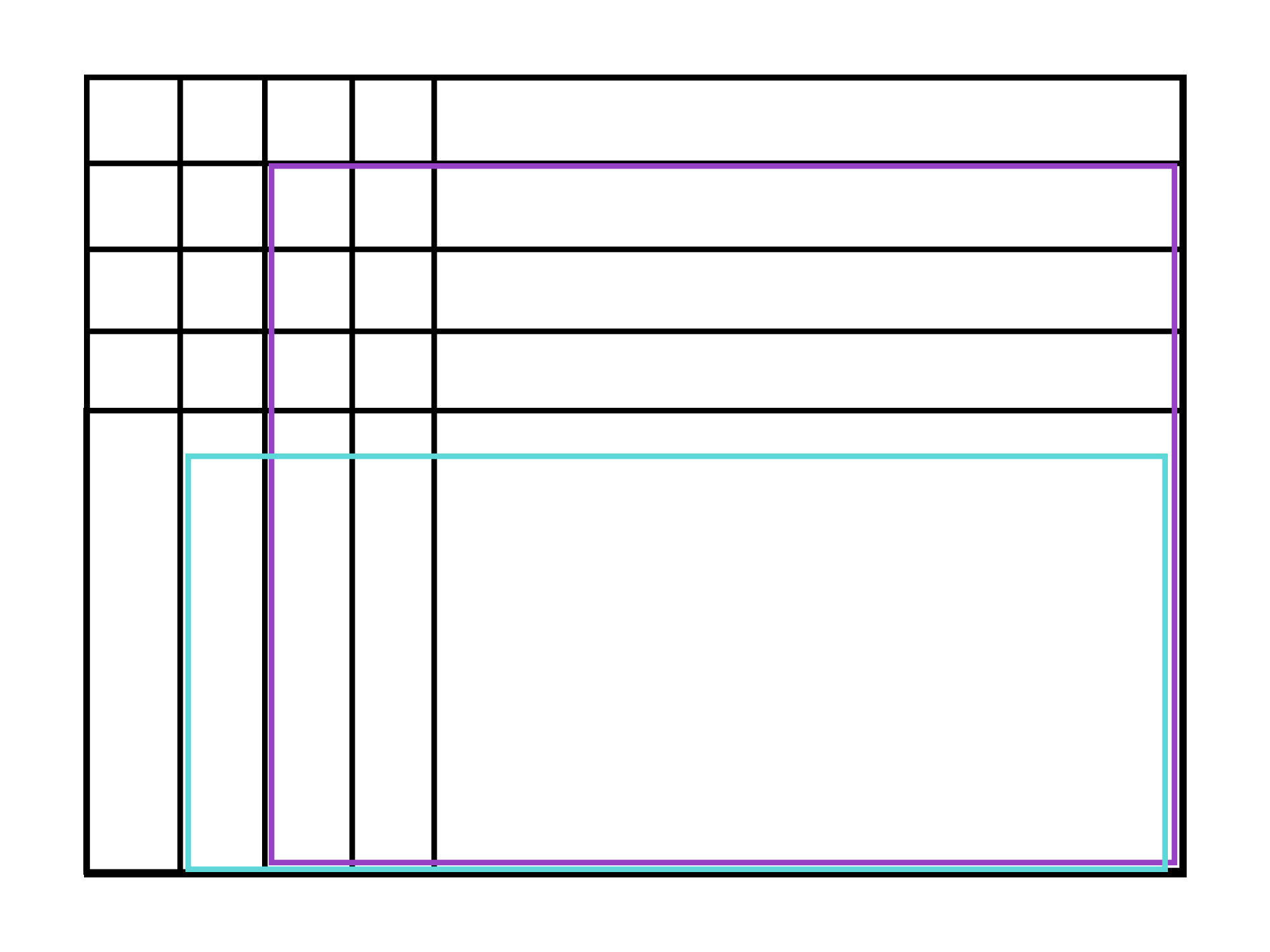
对比上面那种情况，我们只是将蓝色矩形往下平移了一点。具体的计数方式还是跟上面那种情况是一样的。

还要讨论绿色矩形内对角线都互不相同的方案数。

注意要分类讨论 n = m 和 n < m 的 情况。

@代码@

我觉得我的题解可能描述的不是很具体……因为把这道题解释清楚是一件对我来说不太容易的事情……但是我觉得关键的地方我都写上了。

还是请大家多多见谅啦，如果有疑问就留言提出来吧，我会尽力解答的。

#include<cstdio>
#include<algorithm>
using namespace std;
const int MOD = int(1E9) + 7;
int pow_mod(int b, int p) {
    int ret = 1;
    while( p ) {
        if( p & 1 ) ret = 1LL*ret*b%MOD;
        b = 1LL*b*b%MOD;
        p >>= 1;
    }
    return ret;
}
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    if( n > m ) swap(n, m);
    if( n == 1 ) {
        printf("%d\n", pow_mod(2, m));
        return 0;
    }
    else if( n == 2 ) {
        printf("%lld\n", 4LL*pow_mod(3, m-1)%MOD);
        return 0;
    }
    else if( n == 3 ) {
    	printf("%lld\n", 112LL*pow_mod(3, m-n)%MOD);
        return 0;
    }
    else {
        int ans = 0;
        if( n == m ) {
        	ans = (ans + 2LL*pow_mod(4, n-2)%MOD*pow_mod(2, n-1)%MOD)%MOD;
        	ans = (ans + 2LL*5LL*pow_mod(4, n-4)%MOD*pow_mod(2, n-1)%MOD)%MOD;
        	for(int i=4;i<=m;i++) {
	            if( i == m ) ans = (ans + 4LL*3LL*pow_mod(2, n-2)%MOD)%MOD;
	            else ans = (ans + 4LL*5LL*pow_mod(4, n-i-1)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	        }
	        ans = (ans + 3LL*pow_mod(2, n-2))%MOD;
	        for(int i=4;i<=n;i++) {
	            if( i == n ) ans = (ans + 4LL*3LL*pow_mod(2, m-2)%MOD)%MOD;
	            else ans = (ans + 4LL*5LL*pow_mod(4, m-i-1)%MOD*pow_mod(2, m-1)%MOD)%MOD;
	        }
	        ans = (ans + 3LL*pow_mod(2, n-2))%MOD;
		}
		else {
			ans = (ans + 2LL*pow_mod(4, n-2)%MOD*pow_mod(3, m-n)%MOD*pow_mod(2, n-1)%MOD)%MOD;
			ans = (ans + 2LL*5LL*pow_mod(4, n-4)%MOD*pow_mod(3, m-n)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	        for(int i=4;i<=m;i++) {
	            if( i == m ) ans = (ans + 3LL*3LL*pow_mod(2, n-2)%MOD)%MOD;
	            else if( i > n ) ans = (ans + 3LL*4LL*pow_mod(3, m-i-1)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	            else if( i == n ) ans = (ans + 4LL*4LL*pow_mod(3, m-n-1)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	            else if( i < n ) ans = (ans + 4LL*5LL*pow_mod(4, n-i-1)%MOD*pow_mod(3, m-n)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	        }
	        ans = (ans + 3LL*pow_mod(2, n-2))%MOD;
	        for(int i=4;i<=n;i++) {
				if( i == n ) ans = (ans + 4LL*4LL*pow_mod(3, m-n-1)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	            else ans = (ans + 4LL*5LL*pow_mod(4, n-i-1)%MOD*pow_mod(3, m-n)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	        }
	    	ans = (ans + 4LL*pow_mod(3, m-n-1)%MOD*pow_mod(2, n-1)%MOD)%MOD;
	    }
        printf("%d\n", 2LL*ans%MOD);//*2:左上角的填数方式
    }
}