c++ 知道旋转前后矩阵向量值求旋转矩阵c++/c#代码知道两个向量求他们的旋转矩阵

原文作者：aircraft

原文链接：https://www.cnblogs.com/DOMLX/p/12115244.html

知道旋转前后矩阵向量值如何去求旋转矩阵R 的c++/c#代码？？？

因为需要用到矩阵处理库所以需要先配置

一、Eigen库的配置(VS2017)

Eigen库下载： http://eigen.tuxfamily.org/index.php?title=Main_Page
下载文件并解压：

然后在自己的VS工程属性中的这个附加包含进去

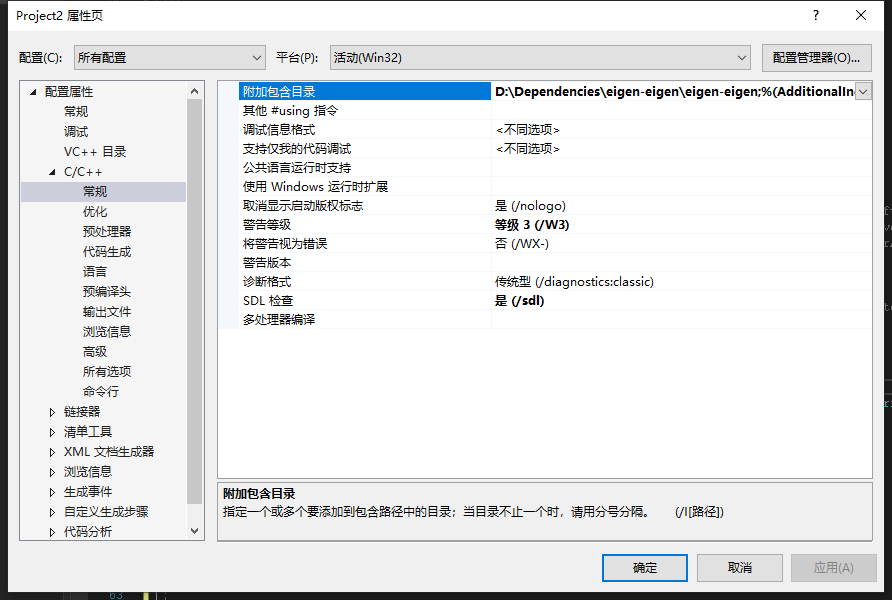
注意看清楚了是D:\Dependencies\eigen-eigen\eigen-eigen; 前面部分是你们自己的路径后面的这个eigen-eigen\eigen-eigen; 代表的意思解压是点击进去选择里面那个名字跟外面一样的

二、实现代码

c++代码：

#include <cmath>

#include <iostream>

#include "Eigen/Dense"

#include "Eigen/LU"

#include "Eigen/Core"

#define PI 3.1415926

//计算旋转角

double calculateAngle(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter)

{

    double ab, a1, b1, cosr;

    ab = vectorBefore.x()*vectorAfter.x() + vectorBefore.y()*vectorAfter.y() + vectorBefore.z()*vectorAfter.z();

    a1 = sqrt(vectorBefore.x()*vectorBefore.x() + vectorBefore.y()*vectorBefore.y() + vectorBefore.z()*vectorBefore.z());

    b1 = sqrt(vectorAfter.x()*vectorAfter.x() + vectorAfter.y()*vectorAfter.y() + vectorAfter.z()*vectorAfter.z());

    cosr = ab / a1 / b1;

    return (acos(cosr) *  / PI);

}

//计算旋转轴

inline Eigen::Vector3d calculateRotAxis(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter)

{

    return Eigen::Vector3d(vectorBefore.y()*vectorAfter.z() - vectorBefore.z()*vectorAfter.y(), \

        vectorBefore.z()*vectorAfter.y() - vectorBefore.x()*vectorAfter.z(), \

        vectorBefore.x()*vectorAfter.y() - vectorBefore.y()*vectorAfter.x());

}

//计算旋转矩阵

void rotationMatrix(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter, Eigen::Matrix3d &rotMatrix)

{

    Eigen::Vector3d vector = calculateRotAxis(vectorBefore, vectorAfter);

    double angle = calculateAngle(vectorBefore, vectorAfter);

    Eigen::AngleAxisd rotationVector(angle, vector.normalized());

    Eigen::Matrix3d rotationMatrix = Eigen::Matrix3d::Identity();

    rotMatrix =  rotationVector.toRotationMatrix();//所求旋转矩阵

}

int main()

{

    Eigen::Matrix3d rotMatrix;

    Eigen::Vector3d vectorBefore(,,);

    Eigen::Vector3d vectorAfter(,,);

    rotationMatrix(vectorBefore, vectorAfter, rotMatrix);

    std::cout << rotMatrix << std::endl;

    system("pause");

    return ;

}

打印结果：

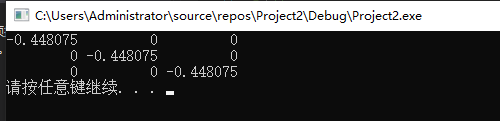
c#代码：

void Calculation(double[] vectorBefore, double[] vectorAfter)

{

    double[] rotationAxis;

    double rotationAngle;

    double[,] rotationMatrix;

    rotationAxis = CrossProduct(vectorBefore, vectorAfter);

    rotationAngle = Math.Acos(DotProduct(vectorBefore, vectorAfter) / Normalize(vectorBefore) / Normalize(vectorAfter));

    rotationMatrix = RotationMatrix(rotationAngle, rotationAxis);

}

double[] CrossProduct(double[] a, double[] b)

{

    double[] c = new double[];

    c[] = a[] * b[] - a[] * b[];

    c[] = a[] * b[] - a[] * b[];

    c[] = a[] * b[] - a[] * b[];

    return c;

}

double DotProduct(double[] a, double[] b)

{

    double result;

    result = a[] * b[] + a[] * b[] + a[] * b[];

    return result;

}

double Normalize(double[] v)

{

    double result;

    result = Math.Sqrt(v[] * v[] + v[] * v[] + v[] * v[]);

    return result;

}

double[,] RotationMatrix(double angle, double[] u)

{

    double norm = Normalize(u);

    double[,] rotatinMatrix = new double[,];

    u[] = u[] / norm;

    u[] = u[] / norm;

    u[] = u[] / norm;

    rotatinMatrix[, ] = Math.Cos(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = u[] * u[] * ( - Math.Cos(angle) - u[] * Math.Sin(angle));

    rotatinMatrix[, ] = u[] * Math.Sin(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = u[] * Math.Sin(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = Math.Cos(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = -u[] * Math.Sin(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = -u[] * Math.Sin(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = u[] * Math.Sin(angle) + u[] * u[] * ( - Math.Cos(angle));

    rotatinMatrix[, ] = Math.Cos(angle) + u[] * u[] * ( - Math.Cos(angle));

    return rotatinMatrix;

}

三、实现原理

1.旋转角度

已知旋转前向量为P, 旋转后变为Q。由点积定义可知：

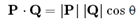可推出P，Q之间的夹角为：

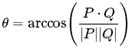
2. 旋转轴

由1中可知，旋转角所在的平面为有P和Q所构成的平面，那么旋转轴必垂直该平面。

假定旋转前向量为a(a1, a2, a3)，旋转后向量为b（b1, b2, b3)。由叉乘定义得：

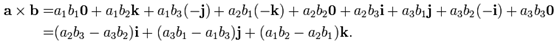
所以旋转轴c(c1, c2, c3)为：

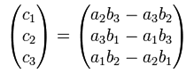
3. 罗德里格旋转公式(Rodrigues' rotation formula)

3.1 公式

已知单位向量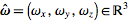，将它旋转θ角。由罗德里格旋转公式，可知对应的旋转矩阵：

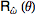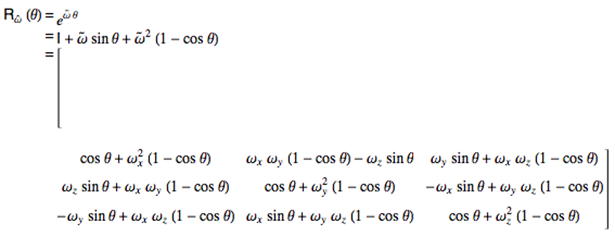
其中I是3x3的单位矩阵，

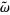是叉乘中的反对称矩阵r：

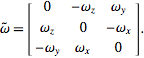
3.2 公式证明

假设在坐标系(x, y, z）中，向量v=ax+by+cz，v绕z轴逆时针旋转θ角后得到新的向量v’。

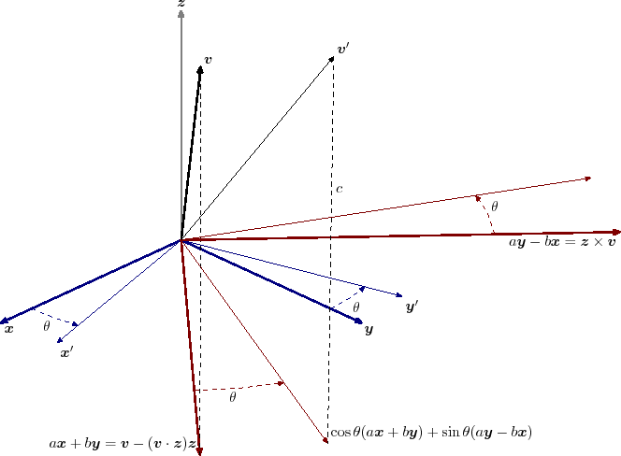
根据2维（x,y)面上的旋转公式可得：

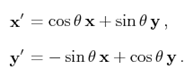
推出：

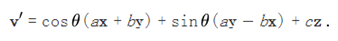已知：

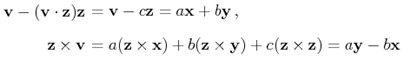将上式带入v’的公式：

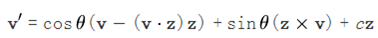将cz替换掉，可得：

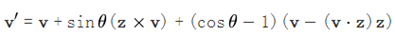
将上式中的叉乘表示为反对称矩阵得：

另外：

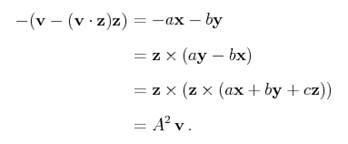
最终可以推出：

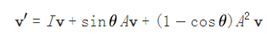
上式即为罗德里格旋转公式。

参考博客：https://www.cnblogs.com/xpvincent/archive/2013/02/15/2912836.html

参考博客里的是c#的实现代码

我是参考完之后改了一个c++的版本出来

若有兴趣交流分享技术，可关注本人公众号，里面会不定期的分享各种编程教程，和共享源码，诸如研究分享关于c/c++,python,前端，后端，opencv,halcon,opengl,机器学习深度学习之类有关于基础编程，图像处理和机器视觉开发的知识