HDU 5727 - Necklace - [全排列+二分图匹配][Hopcroft-Karp算法模板]

题目链接：http://acm.split.hdu.edu.cn/showproblem.php?pid=5727

Problem Description
SJX has 2*N magic gems. N of them have Yin energy inside while others have Yang energy. SJX wants to make a necklace with these magic gems for his beloved BHB. To avoid making the necklace too Yin or too Yang, he must place these magic gems Yin after Yang and Yang after Yin, which means two adjacent gems must have different kind of energy. But he finds that some gems with Yang energy will become somber adjacent with some of the Yin gems and impact the value of the neckless. After trying multiple times, he finds out M rules of the gems. He wants to have a most valuable neckless which means the somber gems must be as less as possible. So he wonders how many gems with Yang energy will become somber if he make the necklace in the best way.

Input
Multiple test cases.
For each test case, the first line contains two integers N(0≤N≤9),M(0≤M≤N∗N), descripted as above.
Then M lines followed, every line contains two integers X,Y, indicates that magic gem X with Yang energy will become somber adjacent with the magic gem Ywith Yin energy.

Output
One line per case, an integer indicates that how many gem will become somber at least.

Sample Input
2 1
1 1
3 4
1 1
1 2
1 3
2 1

Sample Output
1 1

题意：

现有2*N个宝珠，N个阴球，N个阳球；给出M个关系，代表当Xi阴球和Yi阳球连接在一起时，Yi阳球会变得很“失落”；

要求求出最小多少个阳球会变成“失落”的。

 

题解：

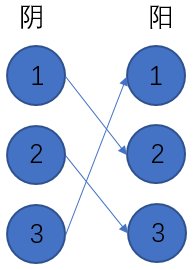假如我们现在有如下的匹配：，就不难得到对应的项链穿法：（如果规定了阴球的排列顺序为1->2->3的话，那么项链的穿法就固定了）

 

那么，如果我们按照题目所给的样例2：

3 4

1 1

1 2

1 3

2 1

做出如下的图：

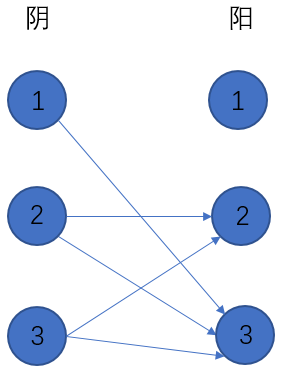（阴球1,2,3对阳球1都会产生“失落”的影响，所以没有一条边连向阳球1；而阴球1会使阳球2“失落”，所以也没有连边。）

我们求出最大匹配，就能得到一个相应的项链穿法：

　　　　　　　　　　

显然，由于一些边的缺少，导致了阳球的失配，所以此时 3 - 最大匹配数 = “失落的”球数

 

当然，这是在固定的阴球顺序下得到的，我们要求得所有可能性中的最小，就需要对阴球进行全排列；

不妨使用STL中的next_permutation函数对阴球进行全排列，下面是next_permutation函数的用法实例：

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
    int num[]={,,};
    do
    {
        cout<<num[]<<" "<<num[]<<" "<<num[]<<endl;
    }while(next_permutation(num,num+));
}

这样，整一道题目的解法就已经相当完整了；

还有一个需要注意的小细节，那就是：

因为项链成环，所以 1 -> 2 -> 3( -> 1 ) 和 2 -> 3 -> 1( -> 2 )其实是相同的项链，不需要重复计算，故我们需要定项链的一个“头”；

对应到全排列时，即保证任意的阴球顺序，都是1号阴球排在第一位，这样就不会产生重复计算了；

AC代码：

 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<algorithm>
 #define MAX 11
 #define INF 0x3f3f3f3f
 using namespace std;
 int n,m,Yin[MAX];
 bool unable[MAX][MAX];

 struct Edge{
     int u,v;
 };
 vector<Edge> E;
 vector<int> G[*MAX];
 int matching[*MAX];
 int vis[*MAX];
 void init(int l,int r)
 {
     E.clear();
     for(int i=l;i<=r;i++) G[i].clear();
 }
 void add_edge(int u,int v)
 {
     E.push_back((Edge){u,v});
     E.push_back((Edge){v,u});
     int _size=E.size();
     G[u].push_back(E.size()-);
     G[v].push_back(E.size()-);
 }
 bool dfs(int u)
 {
     for(int i=,_size=G[u].size();i<_size;i++)
     {
         int v=E[G[u][i]].v;
         if (!vis[v])
         {
             vis[v]=;
             if(!matching[v] || dfs(matching[v]))
             {
                 matching[v]=u;
                 matching[u]=v;
                 return true;
             }
         }
     }
     return false;
 }
 int hungarian()
 {
     int ret=;
     memset(matching,,sizeof(matching));
     for(int i=;i<=n;i++)
     {
         if(!matching[i])
         {
             memset(vis,,sizeof(vis));
             if(dfs(i)) ret++;
         }
     }
     return ret;
 }

 int main()
 {
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         memset(unable,,sizeof(unable));
         for(int i=,a,b;i<=m;i++)
         {
             scanf("%d%d",&a,&b);
             unable[a][b]=;
         }

         if(n== || m==)
         {
             printf("0\n");
             continue;
         }

         for(int i=;i<=n;i++) Yin[i]=i;
         int ans=INF;
         do
         {
             init(,*n);
             for(int i=;i<=n;i++)
             {
                 for(int j=;j<=n;j++)
                 {
                     int a,b;
                     if(i==n) a=Yin[n], b=Yin[];
                     else a=Yin[i], b=Yin[i+];
                     if(unable[j][a]||unable[j][b]) continue;
                     add_edge(i,n+j);
                 }
             }
             ans=min(ans,n-hungarian());
         }while(next_permutation(Yin+,Yin+n+));

         printf("%d\n",ans);
     }
 }

然后是使用了HK算法来求二分图最大匹配的AC代码：

#include<bits/stdc++.h>
#define MAX 11
#define INF 0x3f3f3f3f
using namespace std;
int n,m,Yin[MAX];
bool unable[MAX][MAX];

/*******************************************
Hopcroft-Karp算法：
初始化：edge[][]邻接矩阵,Nx和Ny为左右点个数
左右点编号为1~N,间复杂度为 O( (V^0.5) * E )
*******************************************/
struct Hopcroft_Karp{
    int edge[MAX][MAX],Mx[MAX],My[MAX],Nx,Ny;
    int dx[MAX],dy[MAX],dis;
    bool vis[MAX];
    void init(int uN,int vN)
    {
        Nx=uN, Ny=vN;
        for(int i=;i<=uN;i++) for(int j=;j<=vN;j++) edge[i][j]=;
    }
    void addedge(int u,int v){edge[u][v]=;}
    bool searchP()
    {
        queue<int> Q;
        dis=INF;
        memset(dx,-,sizeof(dx));
        memset(dy,-,sizeof(dy));
        for(int i=;i<=Nx;i++)
        {
            if(Mx[i]==-)
            {
                Q.push(i);
                dx[i]=;
            }
        }
        while(!Q.empty())
        {
            int u=Q.front();Q.pop();
            if(dx[u]>dis) break;
            for(int v=;v<=Ny;v++)
            {
                if(edge[u][v] && dy[v]==-)
                {
                    dy[v]=dx[u]+;
                    if(My[v]==-) dis=dy[v];
                    else
                    {
                        dx[My[v]]=dy[v]+;
                        Q.push(My[v]);
                    }
                }
            }
        }
        return dis!=INF;
    }
    bool dfs(int u)
    {
        for(int v=;v<=Ny;v++)
        {
            if(!vis[v] && edge[u][v] && dy[v]==dx[u]+)
            {
                vis[v]=;
                if(My[v]!=- && dy[v]==dis) continue;
                if(My[v]==- || dfs(My[v]))
                {
                    My[v]=u;
                    Mx[u]=v;
                    return true;
                }
            }
        }
        return false;
    }
    int max_match()
    {
        int ret=;
        memset(Mx,-,sizeof(Mx));
        memset(My,-,sizeof(My));
        while(searchP())
        {
            memset(vis,,sizeof(vis));
            for(int i=;i<=Nx;i++) if(Mx[i]==-) ret+=dfs(i);
        }
        return ret;
    }
}HK;

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(unable,,sizeof(unable));
        for(int i=,a,b;i<=m;i++)
        {
            scanf("%d%d",&a,&b);
            unable[a][b]=;
        }

        if(n== || m==)
        {
            printf("0\n");
            continue;
        }

        for(int i=;i<=n;i++) Yin[i]=i;
        int ans=INF;
        do
        {
            HK.init(n,n);
            for(int i=;i<=n;i++)
            {
                for(int j=;j<=n;j++)
                {
                    int a,b;
                    if(i==n) a=Yin[n], b=Yin[];
                    else a=Yin[i], b=Yin[i+];
                    if(unable[j][a]||unable[j][b]) continue;
                    HK.addedge(i,j);
                }
            }
            ans=min(ans,n-HK.max_match());
        }while(next_permutation(Yin+,Yin+n+));

        printf("%d\n",ans);
    }
}