POJ-2299 Ultra-QuickSort---树状数组求逆序对+离散化

题目链接：

https://vjudge.net/problem/POJ-2299

题目大意：

本题要求对于给定的无序数组，求出经过最少多少次相邻元素的交换之后，可以使数组从小到大有序。

两个数（a, b）的排列，若满足a > b，则称之为一个逆序对。

n < 500,000   0 ≤ a[i] ≤ 999,999,999

解题思路：

由于数据范围大，可以考虑离散化。

为什么要离散化？

离散化的目的就在于将这么多的数字转化成1-500000以内，然后开一个tree树状数组，下标就对应着数值

如何离散化？

从小到大离散化成1-n，比如数组9 1 0 5 4 离散化成5 2 1 4 3，然后就可以用树状数组做了。

开了树状数组，接下来怎么做？

从左往右依次往树状数组中加入元素，每次加入的时候，在对应下标的位置的数字加一，加入之后数一下在这个下标后面有多少个1，就是加入该数字的逆序对的数目

下面进行模拟 5 2 1 4 3，模拟之后你就懂了

最初的树状数组：

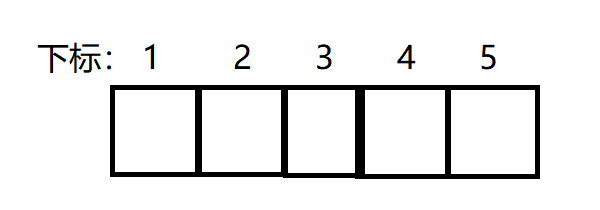
1、首先加入5，此时树状数组的第5个元素+1（红块表示加1），此时5的后面没有元素，所以加入5的逆序对为0，ans = 0

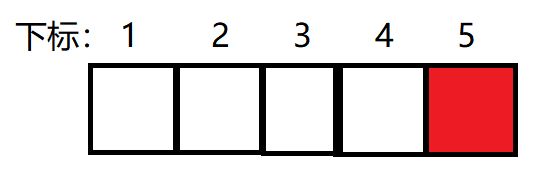
2、加入2，此时第2个元素加1，2的后面有一个红块（表示加一），所以加入2的逆序对为1， ans = 1

3、加入1，此时第1个元素加1，1的后面有两个红块（表示加一），所以加入1的逆序对为2， ans = 3

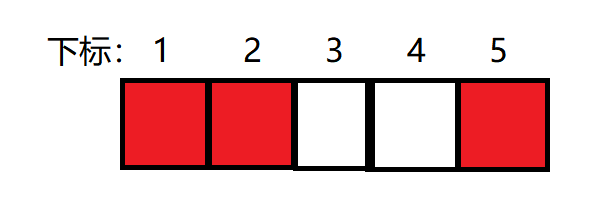
4、加入4，此时第4个元素加1，4的后面有一个红块（表示加一），所以加入4的逆序对为1， ans =4

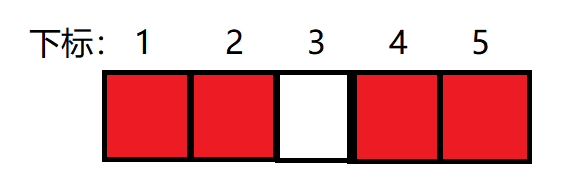
5、加入3，此时第3个元素加1，3的后面有两个红块（表示加一），所以加入3的逆序对为2， ans = 6

利用树状数组可以在o(log(n))的时间复杂度求出当前数字的前缀和，进而可以求出在当前数字后面数字的个数（i-sum(x)）(i表示已经加入的总数字的数目，sum(x)表示小于等于x的数字的数目，它们之差就是大于x的数字的数目)

这样就把逆序对问题和树状数组联系起来了。

还有需要注意的地方：

如果，数据之中有数字相等的情况，离散化应该怎么处理呢？

举个例子 2 2 2 2，如果离散化成1 2 3 4，那么每次加入的时候在树状数组中找比它大的元素个数，求出的逆序对为0，正确，这种处理不会产生冲突

如果离散化成4 3 2 1，求出的解时6，答案错误，所以在离散化的时候，权值小的离散之后的值小，权值相同的，下标在前面的离散后的值小。

小技巧：

用结构体存权值和id，排序之后根据id创建新的离散化后的数组

上代码：

 #include<iostream>
 #include<algorithm>
 #include<set>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 const int maxn =  + ;
 typedef long long ll;
 struct node
 {
     int x, id;
     bool operator < (const node& a)const
     {
         return x < a.x || x == a.x && id < a.id;
         //从小到大排序,如果x相等，那么编号小的排在前面
         //这是因为这样的话之后离散化的时候，编号小的离散化的数字也是小的
         //之后求逆序对时需要按照原来ID顺序一个一个放离散化的数字
         //相同的x最开始放入的值是小的，后面放入的值是大的，这样不会额外增加逆序对
         //比如一个数组2 2 2 2 按照上述方法离散化成1 2 3 4，逆序对为0。
         //如果离散化成4 3 2 1，则逆序对就会求错了
     }
 }a[maxn];
 int b[maxn];
 int tree[maxn];
 int n;
 int lowbit(int x)
 {
     return x & (-x);
 }
 void add(int x, int d)
 {
     while(x <= n)
     {
         tree[x] += d;
         x += lowbit(x);
     }
 }
 ll sum(int x)
 {
     ll ret = ;
     while(x > )//此处等于0会导致无限循环
     {
         ret += tree[x];
         x -= lowbit(x);
     }
     return ret;
 }
 int main()
 {
     while(cin >> n && n)
     {
         memset(tree, , sizeof(tree));
         memset(a, , sizeof(a));
         memset(b, , sizeof(b));
         for(int i = ; i <= n; i++)
         {
             scanf("%d", &a[i].x);
             a[i].id = i;
         }
         sort(a + , a + n + );
         for(int i = ; i <= n; i++)
         {
             b[a[i].id] = i;//离散化操作，根据原来的id，进行大小的编号，从小到大编号1-n
         }
         ll ans = ;
         for(int i = ; i <= n; i++)
         {
             add(b[i], );//将b[i]加入树状数组中
             ans += i - sum(b[i]);//i-sum(b[i])表示目前加入了i个数，其中有sum(b[i])个数字比b[i]小，相减的结果就是目前比b[i]大的数字数目
         }
         cout<<ans<<endl;
     }
     return ;
 }

离散化的另一种方式

之前是从小到大离散化，现在从大到小离散化，9 1 0 5 4 离散化成1 4 5 2 3，那进行树状数组求值的时候，每加入一个数，求前面比它小的数字即可，正好是树状数组的sum函数的作用

比如上述例子

1 4 5 2 3

加入1时，没有比1小的，ans=0

加入4时，有1个比4小，ans = 1;

加入5是，有2个比5小，ans = 3；

。。。。。。

同理，上述的有重复元素的时候2 2 2 2离散化成1 2 3 4的时候是错误的，因为这里是找比该数小的数字，所以1 2 3 4求出逆序对为6，是错误的

离散化成4 3 2 1的话，就是正确的。

上代码：（找不同，好好看看就懂了）

 #include<iostream>
 #include<algorithm>
 #include<set>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 const int maxn =  + ;
 typedef long long ll;
 struct node
 {
     int x, id;
     bool operator < (const node& a)const
     {
         return x > a.x || x == a.x && id > a.id;//这里变啦！！！
     }
 }a[maxn];
 int b[maxn];
 int tree[maxn];
 int n;
 int lowbit(int x)
 {
     return x & (-x);
 }
 void add(int x, int d)
 {
     while(x <= n)
     {
         tree[x] += d;
         x += lowbit(x);
     }
 }
 ll sum(int x)
 {
     ll ret = ;
     while(x > )//此处等于0会导致无限循环
     {
         ret += tree[x];
         x -= lowbit(x);
     }
     return ret;
 }
 int main()
 {
     while(cin >> n)
     {
         memset(tree, , sizeof(tree));
         memset(a, , sizeof(a));
         memset(b, , sizeof(b));
         for(int i = ; i <= n; i++)
         {
             scanf("%d", &a[i].x);
             a[i].id = i;
         }
         sort(a + , a + n + );
         for(int i = ; i <= n; i++)
         {
             b[a[i].id] = i;//离散化操作，根据原来的id，进行大小的编号，从大到小编号1-n
         }
         ll ans = ;
         for(int i = ; i <= n; i++)//还有下面的两行
         {
             ans += sum(b[i]);//下标比b[i]小，但是实际的数字比b[i]大（因为离散化的时候就是数字大的编号小）
             add(b[i], );//要先调用sum，再调用add，因为先调用add的话，求sum的时候把自己也算进去了
         }
         cout<<ans<<endl;
     }
 }