Re.常系数齐次递推

前言

嗯   我之前的不知道多少天看这个的时候到底在干什么呢

为什么那么。。  可能大佬们太强的缘故

最后仔细想想思路那么的emmm

不说了  要落泪了

唔唔唔

---

前置

多项式求逆

多项式除法/取模

---

常系数齐次递推目的

求一个满足k阶齐次线性递推数列a_i的第n项

即: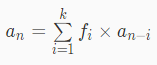 

给出f1--fk,a₀--a_k-1求a_n

N=1e9,K=32000

---

常系数齐次递推主要思路

emmm矩阵快速幂怎么样都应该会的

设转移矩阵为A,st=[a₀,a₁...a_k-2,a_k-1]为初始矩阵

显然a_n=(st*Aⁿ)₀

O(k³logn)和O(k²logklogn)的矩阵快速幂在此范围下显然太暴力了

发现k过大时时间复杂度主要花在矩阵乘法上

考虑如何不用矩阵通过多项式来计算答案

先考虑把Aⁿ转化为A⁰--A^k-1组合出来的和

设Aⁿ=Q(A)*G(A)+R(A)

Q,G,R是以矩阵为x(参数)的多项式

当强制G的多项式的最高次数为k次方

那么可写成Aⁿ=Q(A)*G(A)+c_iA_ⁱ

此时如果再强制试使得G(A)为0时

那么Q(A)*G(A)=0

Aⁿ=c_iA_ⁱ=R(A)

所以c_iA^_i=Aⁿ%G(A)

通过多项式取模就可将Aⁿ转化为c_iA_ⁱ

通过上面的推导发现a_n=(st*A_n)₀=(st*c_iA^_i)₀=(c_iA^_ist)₀

因为我们每次只取矩阵的第0项  每转移一次下一项就往上移一个位置 原来的第0项就去掉

所以A^_ist就等于st_i

最后的a_n=c_ist_i

这样只要找出之前要求的那个G(A)就可以O(k)得出答案了

那么如何求出G(A)

设G(A)=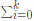g_iAⁱ=0

这里有个我暂时不会的结论

如果递推系数为f₁--f_n

那么g_k-i=f_i,g_k=1

所以最后流程就是

1.求出G(A)

2.用快速幂和多项式取模求出Aⁿ在模G(A)时的余数R(A) 也就是把Aⁿ转化为A¹--A^k的组合

3.计算答案aⁿ=c_ist_i

---

代码

这 时隔多年我中于调出来了一份常数巨大的代码

 #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define C getchar()-48
inline ll read()
{
    ll s=,r=;
    char c=C;
    for(;c<||c>;c=C) if(c==-) r=-;
    for(;c>=&&c<=;c=C) s=(s<<)+(s<<)+c;
    return s*r;
}
const int p=,G=,N=;
int n,k,mx,cs,qvq,tz;
ll rev[N];
ll f[N],st[N],g[N],invg[N];
ll tmp[N],tmp1[N],tmp2[N],tmpa[N],tmpb[N];
ll a[N],ans[N];
inline ll ksm(ll a,ll b)
{
    ll ans=;
    while(b)
    {
        if(b&) ans=(ans*a)%p;
        a=(a*a)%p;
        b>>=;
    }
    return ans;
}
inline void ntt(ll *a,ll n,ll kd)
{
    for(int i=;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=;i<n;i<<=)
    {
        ll gn=ksm(G,(p-)/(i<<));
        for(int j=;j<n;j+=(i<<))
        {
            ll t1,t2,g=;
            for(int k=;k<i;k++,g=g*gn%p)
            {
                t1=a[j+k],t2=g*a[j+k+i]%p;
                a[j+k]=(t1+t2)%p,a[j+k+i]=(t1-t2+p)%p;
            }
        }
    }
    if(kd==) return;
    ll ny=ksm(n,p-);
    reverse(a+,a+n);
    for(int i=;i<n;i++) a[i]=a[i]*ny%p;
}
inline void cl(ll *a,ll *b,ll n,ll m,ll len,ll w)
{
    for(int i=;i<len;i++) tmp1[i]=i<n?a[i]:;
    for(int i=;i<len;i++) tmp2[i]=i<m?b[i]:;
    for(int i=;i<len;i++) rev[i]=(rev[i>>]>>)|((i&)<<(w-));
}
inline void polyinv(ll *a,ll *b,ll ed)
{
    b[]=ksm(a[],p-);
    for(int k=,j=;k<=(ed<<);k<<=,j++)
    {
        ll len=k<<;
        cl(a,b,k,k,len,j+);
        ntt(tmp1,len,);ntt(tmp2,len,);
        for(int i=;i<len;i++) b[i]=tmp2[i]*(2ll-tmp1[i]*tmp2[i]%p+p)%p;
        ntt(b,len,-);
        for(int i=k;i<len;i++) b[i]=;
    }
}
inline void polymul(ll *a,ll *b,ll *c,ll n,ll m)
{
    ll len=,w=;
    while(len<=(n+m)) len<<=,w++;
    cl(a,b,n,m,len,w);
    ntt(tmp1,len,);ntt(tmp2,len,);
    for(int i=;i<len;i++) c[i]=tmp1[i]*tmp2[i]%p;
    ntt(c,len,-);
}
inline void polymod(ll *a,ll n=mx<<,ll m=k)
{
    int ed=(mx<<);while(a[--ed]==);if(ed<k) return; 

    n=ed;
    reverse(a,a++n);
    polymul(a,invg,tmpa,n+,n-m+);
    reverse(tmpa,tmpa+n-m+);
    reverse(a,a++n);

    polymul(g,tmpa,tmpb,m+,n-m+);
    for(int i=;i<k;i++) a[i]=(a[i]-tmpb[i]+p)%p;
    for(int i=k;i<=ed;i++)a[i]=;
    for(int i=;i<(mx<<);i++) tmpa[i]=tmpb[i]=;
}
int main()
{
    n=read(),k=read();mx=,cs=;
    while(mx<=k) mx<<=,cs++;
    for(int i=;i<=k;i++) f[i]=read(),f[i]=f[i]<?f[i]+p:f[i];
    for(int i=;i<k;i++) st[i]=read(),st[i]=st[i]<?st[i]+p:st[i];
    for(int i=;i<=k;i++) g[k-i]=p-f[i];g[k]=;
    for(int i=;i<=k;i++) tmp[i]=g[i];

    reverse(tmp,tmp++k);
    polyinv(tmp,invg,mx);
    for(int i=mx;i<=(mx<<);i++) invg[i]=;
    for(int i=;i<=k;i++) tmp[i]=;
    for(int i=;i<(mx<<);i++) rev[i]=(rev[i>>]>>)|((i&)<<(cs+-));
    ans[]=;a[]=;
    while(n)
    {
        if(n&){polymul(ans,a,ans,k,k); polymod(ans);}
        polymul(a,a,a,k,k); polymod(a);
        n>>=;
    }
    for(int i=;i<k;i++) qvq=(qvq+ans[i]*st[i])%p;
    cout<<qvq;
    return ;
}