Python----简单线性回归

简单线性回归

　　　　1、研究一个自变量(X)和一个因变量（y）的关系

　　 　 　　简单线性回归模型定义：y=β₀₊β₁x+ε

　　　　简单线性回归方程：E(y)=β₀+β₁x

　　　　　　其中：

　　　　　　β₀为回归线的截距

　　　　　　β₁为回归线的斜率

　　　　　　通过训练数据，求取出估计参数建立的直线方程：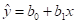

　　　　　　实际编程时，主要是根据已知训练数据，估计出β₀和β1的值b₀和b1

　　　　2、举例：

　　　　　　　　

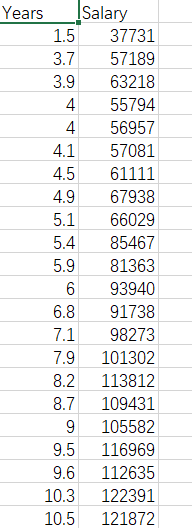
　　　　　实际代码：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

dataset = pd.read_csv('Data.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 1].values

#将数据分成训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1/3, random_state = 0)

#Simple Linear Regression对应机器；拟合对应学习
#创建简单回归器，并且用训练集拟合简单线性回归器
from sklearn.linear_model import LinearRegression#导入类sklearn库里面的LinearRegression线性回归
regressor = LinearRegression()#创建对象
regressor.fit(X_train, y_train)#用训练集的数据拟合

#预测测试集的因变量为多少，并且让预测结果和测试结果进行比较
y_pred = regressor.predict(X_test)#y_pred预测结果，regressor回归器

#画出训练集的实际结果以及回归器的预测结果
plt.scatter(X_train, y_train, color = 'red')#第一个：x轴，自变量；第二个：y轴的值；第三个：为点涂色
plt.plot(X_train, regressor.predict(X_train), color = 'blue')#回归器的预测结果，以线的方式表示；第一个：x轴，自变量；第二个：y轴对应的值，及回归器的预测结果；第三个：为线涂色
plt.title('Salary VS Experience (training set)')#为图像加标题
plt.xlabel('Years of Experience')#为x轴加标签
plt.ylabel('Salary')#为y轴加标签
plt.show()#显示图像

#画出测试集的实际结果以及回归器的预测结果
plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')#回归器针对训练集做拟合的，所以regressor.predict(X_train)无需改动
plt.title('Salary VS Experience (test set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()

   

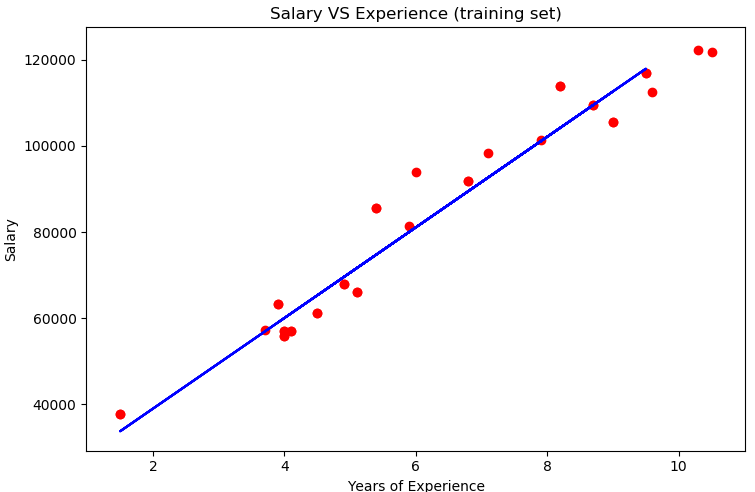
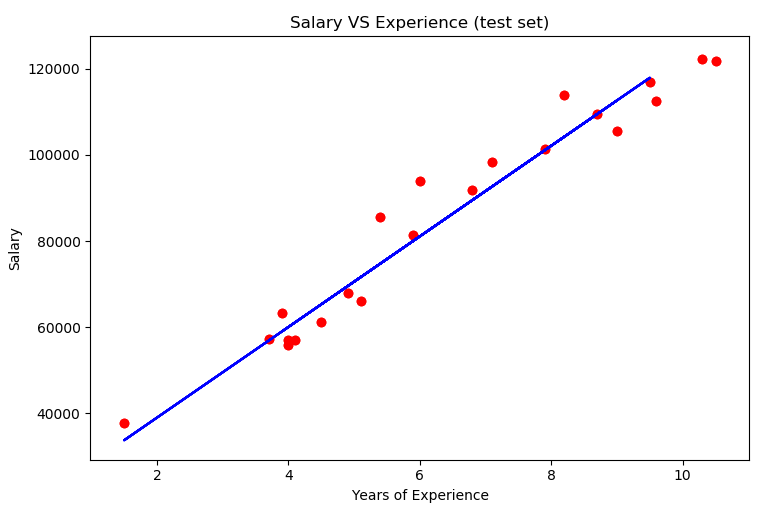
　　红色表示实际结果，蓝色表示预测结果