关联分析：FP-Growth算法

　　关联分析又称关联挖掘，就是在交易数据、关系数据或其他信息载体中，查找存在于项目集合或对象集合之间的频繁模式、关联、相关性或因果结构。关联分析的一个典型例子是购物篮分析。通过发现顾客放入购物篮中不同商品之间的联系，分析顾客的购买习惯。比如，67%的顾客在购买尿布的同时也会购买啤酒。通过了解哪些商品频繁地被顾客同时购买，可以帮助零售商制定营销策略。关联分析也可以应用于其他领域，如生物信息学、医疗诊断、网页挖掘和科学数据分析等。

1. 问题定义

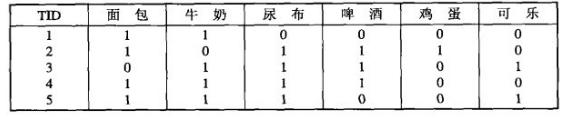
图1 购物篮数据的二元表示

　　图1表示顾客的购物篮数据，其中每一行是每位顾客的购物记录，对应一个事务，而每一列对应一个项。令I={i₁, i₂, ... , i_d}是购物篮数据中所有项的集合，而T={t₁, t₂, ... , t_N}是所有事务的集合。每个事务t_i包含的项集都是I的子集。在关联分析中，包含0个或多个项的集合被称为项集（itemset）。所谓的关联规则是指形如X→Y的表达式，其中X和Y是不相交的项集。在关联分析中，有两个重要的概念——支持度（support）和置信度（confidence）。支持度确定规则可以用于给定数据集的频繁程度，而置信度确定Y在包含X的事务中出现的频繁程度。支持度（s）和置信度（c）这两种度量的形式定义如下：

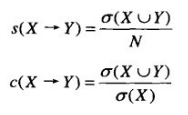
公式1

　　其中，N是事务的总数。关联规则的支持度很低，说明该规则只是偶然出现，没有多大意义。另一方面，置信度可以度量通过关联规则进行推理的可靠性。因此，大多数关联分析算法采用的策略是：

（1）频繁项集产生：其目标是发现满足最小支持度阈值的所有项集，这些项集称作频繁项集。

（2）规则的产生：其目标是从上一步发现的频繁项集中提取所有高置信度的规则，这些规则称作强规则。

2. 构建FP-tree

　　FP-growth算法通过构建FP-tree来压缩事务数据库中的信息，从而更加有效地产生频繁项集。FP-tree其实是一棵前缀树，按支持度降序排列，支持度越高的频繁项离根节点越近，从而使得更多的频繁项可以共享前缀。

图2 事务型数据库

　　图2表示用于购物篮分析的事务型数据库。其中，a，b，...，p分别表示客户购买的物品。首先，对该事务型数据库进行一次扫描，计算每一行记录中各种物品的支持度，然后按照支持度降序排列，仅保留频繁项集，剔除那些低于支持度阈值的项，这里支持度阈值取3，从而得到<(f:4)，(c:4)，(a:3)，(b:3)，(m:3，(p:3)>（由于支持度计算公式中的N是不变的，所以仅需要比较公式中的分子）。图2中的第3列展示了排序后的结果。

　　FP-tree的根节点为null，不表示任何项。接下来，对事务型数据库进行第二次扫描，从而开始构建FP-tree：

　　第一条记录<f，c，a，m，p>对应于FP-tree中的第一条分支<(f:1)，(c:1)，(a:1)，(m:1)，(p:1)>：

图3 第一条记录

　　由于第二条记录<f，c，a，b，m>与第一条记录有相同的前缀<f，c，a>，因此<f，c，a>的支持度分别加一，同时在(a:2)节点下添加节点(b:1)，(m:1)。所以，FP-tree中的第二条分支是<(f:2)，(c:2)，(a:2)，(h:1)，(m:1)>：

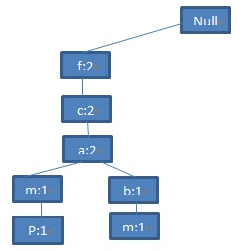
图4 第二条记录

　　第三条记录<f，b>与前两条记录相比，只有一个共同前缀<f>，因此，只需要在(f:3)下添加节点<b:1>：

图5 第三条记录

　　第四条记录<c，b，p>与之前所有记录都没有共同前缀，因此在根节点下添加节点(c:1)，(b:1)，(p:1)：

图6 第四条记录

　　类似地，将第五条记录<f，c，a，m，p>作为FP-tree的一个分支，更新相关节点的支持度：

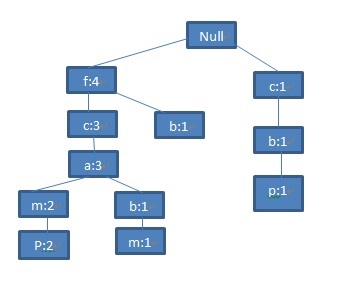
图7 第五条记录

　　为了便于对整棵树进行遍历，建立一张项的头表（an item header table）。这张表的第一列是按照降序排列的频繁项。第二列是指向该频繁项在FP-tree中节点位置的指针。FP-tree中每一个节点还有一个指针，用于指向相同名称的节点：

图8 FP-tree

　　综上，FP-tree的节点可以定义为：

class TreeNode {

private:
    String name; // 节点名称
    int count; // 支持度计数
    TreeNode *parent; // 父节点
    Vector<TreeNode *> children; // 子节点
    TreeNode *nextHomonym; // 指向同名节点

    ...
}

3. 从FP-tree中挖掘频繁模式（Frequent Patterns）

　　我们从头表的底部开始挖掘FP-tree中的频繁模式。在FP-tree中以p结尾的节点链共有两条，分别是<(f:4)，(c:3)，(a:3)，(m:2)，(p:2)>和<(c:1)，(b:1)，(p:1)>。其中，第一条节点链表表示客户购买的物品清单<f，c，a，m，p>在数据库中共出现了两次。需要注意到是，尽管<f，c，a>在第一条节点链中出现了3次，单个物品<f>出现了4次，但是它们与p一起出现只有2次，所以在条件FP-tree中将<(f:4)，(c:3)，(a:3)，(m:2)，(p:2)>记为<(f:2)，(c:2)，(a:2)，(m:2)，(p:2)>。同理，第二条节点链表示客户购买的物品清单<c，b，p>在数据库中只出现了一次。我们将p的前缀节点链<(f:2)，(c:2)，(a:2)，(m:2)>和<(c:1)，(b:1)>称为p的条件模式基（conditional pattern base）。我们将p的条件模式基作为新的事务数据库，每一行存储p的一个前缀节点链，根据第二节中构建FP-tree的过程，计算每一行记录中各种物品的支持度，然后按照支持度降序排列，仅保留频繁项集，剔除那些低于支持度阈值的项，建立一棵新的FP-tree，这棵树被称之为p的条件FP-tree：

图9 p的条件FP-tree

　　从图9可以看到p的条件FP-tree中满足支持度阈值的只剩下一个节点(c:3)，所以以p结尾的频繁项集有(p:3)，(cp:3)。由于c的条件模式基为空，所以不需要构建c的条件FP-tree。

　　在FP-tree中以m结尾的节点链共有两条，分别是<(f:4)，(c:3)，(a:3)，(m:2)>和<(f:4)，(c:3)，(a:3)，(b:1)，(m:1)>。所以m的条件模式基是<(f:2)，(c:2)，(a:2)>和<(f:1)，(c:1)，(a:1)，(b:1)>。我们将m的条件模式基作为新的事务数据库，每一行存储m的一个前缀节点链，计算每一行记录中各种物品的支持度，然后按照支持度降序排列，仅保留频繁项集，剔除那些低于支持度阈值的项，建立m的条件FP-tree:

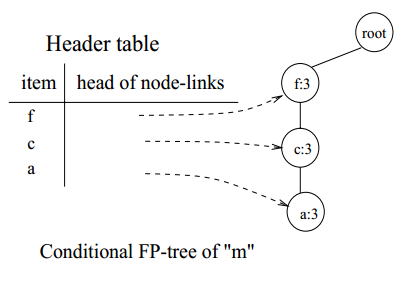
图10 m的条件FP-tree

　　与p不同，m的条件FP-tree中有3个节点，所以需要多次递归地挖掘频繁项集mine(<(f:3)，(c:3)，(a:3)|(m:3)>)。按照<(a:3)，(c:3)，(f:3)>的顺序递归调用mine(<(f:3)，(c:3)|a，m>)，mine(<(f:3)|c，m>)，mine(null|f，m)。由于(m:3)满足支持度阈值要求，所以以m结尾的频繁项集有{(m:3)}。

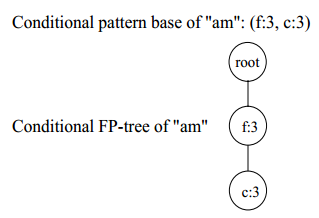
图11 节点(a，m)的条件FP-tree

　　从图11可以看出，节点(a，m)的条件FP-tree有2个节点，需要进一步递归调用mine(<(f:3)|c，a，m>)和mine(<null|f，a，m>)。进一步递归mine(<(f:3)|c，a，m>)生成mine(<null|f，c，a，m>)。因此，以(a，m)结尾的频繁项集有{(am:3)，(fam:3)，(cam:3)，(fcam:3)}。

　　

图 12 节点(c，m)的条件FP-tree

　　从图12可以看出，节点(c，m)的条件FP-tree只有1个节点，所以只需要递归调用mine(<null|f，c，m>)。因此，以(c，m)结尾的频繁项集有{(cm:3)，(fcm:3)}。同理，以(f，m)结尾的频繁项集有{(fm:3)}。

　　在FP-tree中以b结尾的节点链共有三条，分别是<(f:4)，(c:3)，(a:3)，(b:1)>，<(f:4)，(b:1)>和<(c:1)，(b:1)>。由于节点b的条件模式基<(f:1)，(c:1)，(a:1)>，<(f:1)>和<(c:1)>都不满足支持度阈值，所以不需要再递归。因此，以b结尾的频繁项集只有(b:3)。

　　同理可得，以a结尾的频繁项集{(fa:3)，(ca:3)，(fca:3)，(a:3)}，以c结尾的频繁项集{(fc:3)，(c:4)}，以f结尾的频繁项集{(f:4)}。

4. 算法实现

声明FP-tree节点：

class TreeNode
{

    //Constructors-Destructors
public:
    TreeNode();
    TreeNode(string);
    ~TreeNode();

    //Member variables
private:
    string nodeName;
    int supportCount;
    TreeNode *parentNode;
    vector<TreeNode *> childNodeList;
    TreeNode *nextHomonymNode;

    //Member functions
public:

    string getName();
    void setName(string);

    int getSupportCount() const;
    void setSupportCount(int);

    TreeNode* getParentNode() const;
    void setParentNode(TreeNode*);

    vector<TreeNode*> getChildNodeList() const;
    void addChild(TreeNode*);
    TreeNode* findChildNode(string) const;
    void setChildren(vector<TreeNode*>);
    void printChildrenNames() const;

    TreeNode* getNextHomonym() const;
    void setNextHomonym(TreeNode *nextHomonym);

    void countIncrement(int);
};

构建HeaderTable：

//HeaderTable存储事务数据库的数据
vector<TreeNode*> FPTree::buildHeaderTable(vector<vector<string>> transRecords)
{
    vector<TreeNode*> F1; //存储满足支持度阈值的节点，并按照支持度降序排列，支持度相等的情况下按照字母顺序排序，所以构建的FP-tree与论文有所不同，但是最终生成的频繁项集是一样的
    if (transRecords.size() > )
    {
        map<string, TreeNode*> mp;

        //calculate supportCount of every transRecords
        for (vector<string> record : transRecords)
        {
            for (string item : record)
            {
                //if item not in map, put item into map and set supportCount one
                if (mp.find(item) == mp.end())
                {
                    TreeNode *node = new TreeNode(item);
                    node->setSupportCount();
                    mp.insert(map<string, TreeNode*>::value_type(item, node));
                }

                //if item in map, supportCount plus one
                else
                {
                    mp.find(item)->second->countIncrement();
                }
            }
        }

        //put TreeNodes whose supportCount greater than minSupportThreshold into vector F1
        for (auto iterator = mp.begin(); iterator != mp.end(); iterator++)
        {
            if (iterator->second->getSupportCount() >= minSupportThreshold)
            {
                //cout << "iterator->second = " << iterator->second->getSupportCount() << endl;
                F1.push_back(iterator->second);
            }
        }

        //sort vector F1 by supportCount
        sort(F1.begin(), F1.end(), sortBySupportCount);
    }
    return F1;
}

构建FP-tree：

TreeNode* FPTree::buildTree(vector<vector<string>> transRecords, vector<TreeNode*> F1)
{

    TreeNode *root = new TreeNode(); //根节点root
    for (vector<string> transRecord : transRecords)
    {
        //拷贝transRecord到record
        vector<string> record;
        for (auto iter = transRecord.begin(); iter != transRecord.end(); iter++)
        {
            record.push_back(*iter);
        }

        record = sortedByF1(record, F1); //根据F1中存储的频繁项集，将record按照支持度降序排列，并且仅保留频繁项集，剔除那些低于支持度阈值的项

//顺序比较record中的节点和FP-tree中的节点，如果record中的节点已经存在于FP-tree中，将该节点的支持度加一，继续比较下一个节点，否则调用addNodes来添加剩余节点到FP-tree中
        TreeNode *subTreeRoot = root;
        TreeNode *tmpRoot = nullptr;
        if (!root->getChildNodeList().empty())
        {
            while (!record.empty() && (tmpRoot = subTreeRoot->findChildNode(*(record.begin()))) != nullptr)
            {
                tmpRoot->countIncrement();
                subTreeRoot = tmpRoot;
                record.erase(record.begin());
            }
        }
        addNodes(subTreeRoot, &record, F1);
    }
    return root;
}

添加节点：

void FPTree::addNodes(TreeNode *ancestor, vector<string> *record, vector<TreeNode*> F1)
{
    if (!record->empty())
    {
        while (!record->empty())
        {
            string item = *(record->begin());
            record->erase(record->begin());
            TreeNode *leafNode = new TreeNode(item);
            leafNode->setSupportCount();
            leafNode->setParentNode(ancestor);
            ancestor->addChild(leafNode);

            for (TreeNode *f1 : F1)
            {
                if (f1->getName() == item)
                {
                    while (f1->getNextHomonym() != NULL)
                    {
                        f1 = f1->getNextHomonym();
                    }

                    f1->setNextHomonym(leafNode);
                    break;
                }
            }

            addNodes(leafNode, record, F1);
        }
    }
}

sortedByF1：

vector<string> FPTree::sortedByF1(vector<string> transRecord, vector<TreeNode*> F1)
{
    //如果item是频繁项，则一定对应于F1中的序号，按照该序号对item进行排序，存储到rest中
    map<string, int> mp;
    for (string item : transRecord)
    {
        for (int i = ; i < F1.size(); i++)
        {
            TreeNode *tNode = F1[i];
            if (tNode->getName() == item)
            {
                mp.insert(map<string, int>::value_type(item, i));
            }
        }
    }
    vector<pair<string, int>> vec;
    for (auto iterator = mp.begin(); iterator != mp.end(); iterator++)
    {
        vec.push_back(make_pair(iterator->first, iterator->second));
    }
    sort(vec.begin(), vec.end(), sortByF1);
    vector<string> rest;
    for (auto iterator = vec.begin(); iterator != vec.end(); iterator++)
    {
        rest.push_back((*iterator).first);
    }
    return rest;
}

递归调用FP-Growth挖掘频繁项：

//postPattern存储后缀，比如从HeaderTable中的p节点开始挖掘频繁项时，postPattern为p
void FPTree::FPGrowth(vector<vector<string>> transRecords, vector<string> postPattern)
{
    vector<TreeNode*> headerTable = buildHeaderTable(transRecords); //构建headerTable
    TreeNode *treeRoot = buildTree(transRecords, headerTable); //构建FP-tree

//递归退出条件：根节点没有孩子节点
    if (treeRoot->getChildNodeList().size() == )
    {
        return;
    }
//输出频繁项集
    if (!postPattern.empty())
    {
        for (TreeNode *header : headerTable)
        {
            cout << header->getSupportCount() << ends << header->getName() << ends;
            for (string str : postPattern)
            {
                cout << str << ends;
            }
            cout << endl;
        }
    }

//遍历headerTable
    for (TreeNode *header : headerTable)
    {
        vector<string> newPostPattern;
        newPostPattern.push_back(header->getName());

//存储原先的后缀
        if (!postPattern.empty())
        {
            for (string str : postPattern)
            {
                newPostPattern.push_back(str);
            }
        }
//newTransRecords存储前缀节点链
        vector<vector<string>> newTransRecords;
        TreeNode *backNode = header->getNextHomonym();

//通过getNextHomonym遍历同名节点，通过getParentNode获取前缀节点链
        while (backNode != nullptr)
        {
            int supportCount = backNode->getSupportCount();
            vector<string> preNodes;
            TreeNode *parent = backNode; 
            while ((parent = parent->getParentNode())->getName().length() != )
            {
                preNodes.push_back(parent->getName());
            }            while (supportCount-- > )
            {
                newTransRecords.push_back(preNodes);
            }
            backNode = backNode->getNextHomonym();
        }
        FPGrowth(newTransRecords, newPostPattern); //递归构建条件FP-tree
    }
}

5. 讨论

　　在韩家炜教授提出FP-growth算法之前，关联分析普遍采用Apriori及其变形算法。但是，Apriori及其变形算法需要多次扫描数据库，并需要生成指数级的候选项集，性能并不理想。FP-growth算法提出利用了高效的数据结构FP-tree，不再需要多次扫描数据库，同时也不再需要生成大量的候选项。

　　对于单路径的FP-tree其实不需要递归，通过排列组合可以直接生成。韩家炜教授在其论文中提到了针对单路径的优化算法。论文中也提到了面对大数据时，如何调整FP-growth算法使之适应数据量。

6. 参考资料

[1] Mining Frequent Patterns without Candidate Generation. Jiawei Han, Jian Pei, and Yiwen Yin. Data Mining and Knowledge Discovery. Volume 8 Issue 1. January 2004. [PDF]

[2] Frequent Pattern 挖掘之二(FP Growth算法). yfx416. Software Engineer in NRC. 2011. [Link]

[3] FP-Tree算法的实现. Orisun. 华夏35度. 2011. [Link]