机器学习-kNN-数据归一化

一、为什么需要数据归一化

　　不同数据之间因为单位不同，导致数值差距十分大，容易导致预测结果被某项数据主导，所以需要进行数据的归一化。

　　解决方案：将所有数据映射到同一尺度

二、最值归一化 normalization

　　最值归一化：把所有数据映射到0-1之间

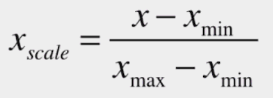
　　适用于分布有明显边界的情况；受outlier影响较大

import numpy as np

import matplotlib.pyplot as plt

x = np.random.randint(0,100,100)

# 一维矩阵的最值归一化

print((x - np.min(x)) / (np.max(x) - np.min(x))) #最值归一化

# 二维矩阵中分别对每列进行最值归一化

x = np.random.randint(0,100,(50,2))

x = np.array(x,dtype=float)

x[:,0] = (x[:,0] - np.min(x[:,0])) / (np.max(x[:,0]) - np.min(x[:,0]))

x[:,1] = (x[:,1] - np.min(x[:,1])) / (np.max(x[:,1]) - np.min(x[:,1]))

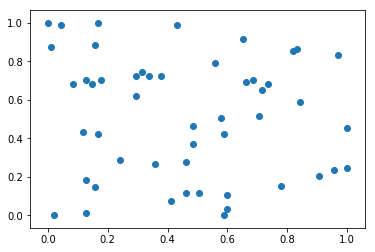
# 绘制散点图

plt.scatter(x[:,0],x[:,1])

plt.show()

# 第0列的均值和方差

print(np.mean(x[:,0]))

print(np.std(x[:,0]))

# 第1列的均值和方差

print(np.mean(x[:,1]))

print(np.std(x[:,1]))

输出结果：

[0.37373737 0.77777778 0.47474747 0.17171717 0.82828283 0.13131313

 0.66666667 1.         0.73737374 0.26262626 0.3030303  0.88888889

 0.85858586 0.80808081 0.92929293 0.64646465 0.97979798 0.16161616

 0.7979798  0.64646465 0.95959596 0.29292929 0.90909091 0.8989899

 0.29292929 0.62626263 0.65656566 0.35353535 0.85858586 0.8989899

 0.03030303 0.76767677 0.75757576 0.8989899  0.26262626 0.82828283

 0.72727273 0.77777778 0.16161616 0.18181818 0.81818182 0.19191919

 0.11111111 0.90909091 0.17171717 0.04040404 0.52525253 0.

 0.34343434 0.88888889 0.07070707 0.82828283 0.01010101 0.63636364

 0.56565657 0.1010101  0.05050505 0.15151515 0.91919192 0.03030303

 0.96969697 0.26262626 0.06060606 0.06060606 0.66666667 0.74747475

 0.14141414 0.64646465 0.77777778 0.90909091 0.47474747 0.72727273

 0.96969697 0.76767677 0.23232323 0.26262626 0.54545455 0.41414141

 0.11111111 0.38383838 0.66666667 0.12121212 0.64646465 0.27272727

 0.21212121 0.21212121 0.84848485 0.71717172 0.5959596  0.56565657

 0.07070707 0.77777778 0.95959596 0.90909091 0.42424242 0.

 0.94949495 0.95959596 0.41414141 0.68686869]

0.4574736842105262

0.29314011096016795

0.5129896907216495

0.3081736973516696

三、均值方差归一化 standardization

　　均值方差归一化：把所有数据归一到均值为0方差为1的分布中

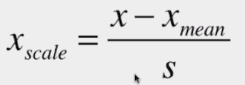
　　适用于数据分布没有明显的边界，有可能存在极端数据值

import numpy as np

import matplotlib.pyplot as plt

# 二维矩阵中分别对每列进行均值方差归一化

x2 = np.random.randint(0,100,(50,2))

x2 = np.array(x2,dtype=float)

x2[:,0] = (x2[:,0] - np.mean(x2[:,0])) / np.std(x2[:,0])

x2[:,1] = (x2[:,1] - np.mean(x2[:,1])) / np.std(x2[:,1])

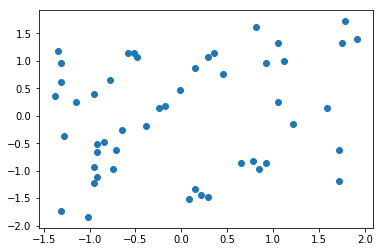
plt.scatter(x2[:,0],x2[:,1])

plt.show()

#打印对应列的均值和方差

print(np.mean(x2[:,0]))

print(np.std(x2[:,0]))

print(np.mean(x2[:,1]))

print(np.std(x2[:,1]))

运行结果：

7.348288644237755e-17

1.0

8.104628079763643e-17

0.9999999999999999

四、对测试数据进行归一化

　　利用scikit-learn中的StandardScaler对数据进行均值方差归一化演示：

import numpy as np

from sklearn import datasets

iris = datasets.load_iris()

x = iris.data

y = iris.target

from sklearn.model_selection import train_test_split

#创建训练数据集和测试数据集

x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state = 666)

from sklearn.preprocessing import StandardScaler

# 构造均值方差归一化对象

standardScaler = StandardScaler()

# 把自身返回回来，现在standardScaler中存放了计算均值方差归一化的关键信息

standardScaler.fit(x_train)

# 均值

print('训练数据均值：',standardScaler.mean_ )

# 描述数据分布范围 包括：方差 标准差等

print('训练数据方差：',standardScaler.scale_)

# 对训练数据进行归一化处理

x_train = standardScaler.transform(x_train)

# 对测试数据进行归一化处理，并赋值给 x_test_standard

x_test_standard = standardScaler.transform(x_test)

from sklearn.neighbors import KNeighborsClassifier

# 创建一个kNN分类器

knn_clf = KNeighborsClassifier(n_neighbors=3)

# 将均值方差归一化后的数据进行写入

knn_clf.fit(x_train,y_train)

# 计算分类器准确度

print("测试数据经过均值方差归一化后 准确度：",knn_clf.score(x_test_standard,y_test))

# 测试数据集没有进行归一化处理

print("测试数据未经过均值方差归一化后 准确度：",knn_clf.score(x_test,y_test))