LeetCode：范围求和||【598】

LeetCode：范围求和||【598】

题目描述

给定一个初始元素全部为 0，大小为 m*n 的矩阵 M 以及在 M 上的一系列更新操作。

操作用二维数组表示，其中的每个操作用一个含有两个正整数 a 和 b 的数组表示，含义是将所有符合 0 <= i < a 以及 0 <= j < b 的元素 M[i][j] 的值都增加 1。

在执行给定的一系列操作后，你需要返回矩阵中含有最大整数的元素个数。

示例 1:

输入:
m = 3, n = 3
operations = [[2,2],[3,3]]
输出: 4
解释:
初始状态, M =
[[0, 0, 0],
 [0, 0, 0],
 [0, 0, 0]]

执行完操作 [2,2] 后, M =
[[1, 1, 0],
 [1, 1, 0],
 [0, 0, 0]]

执行完操作 [3,3] 后, M =
[[2, 2, 1],
 [2, 2, 1],
 [1, 1, 1]]

M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

注意:

1. m 和 n 的范围是 [1,40000]。
2. a 的范围是 [1,m]，b 的范围是 [1,n]。
3. 操作数目不超过 10000。

题目分析

　　

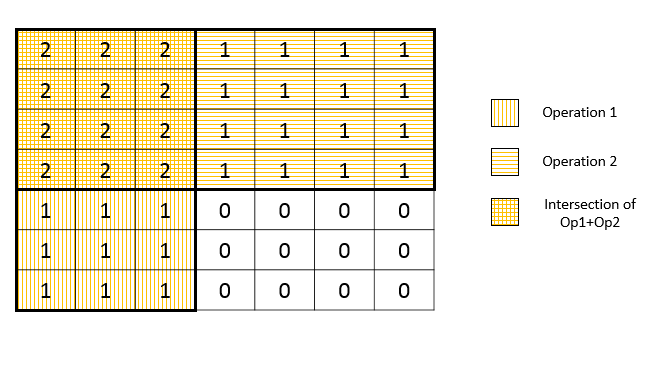
Java题解

public class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        for(int[] op:ops)
        {
            m=Math.min(op[0],m);
            n=Math.min(op[1],n);
        }
        return m*n;
    }
}