SDUT 3364 数据结构实验之图论八：欧拉回路

数据结构实验之图论八：欧拉回路

Time Limit: 1000MS Memory Limit: 65536KB

Submit Statistic

Problem Description

在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。

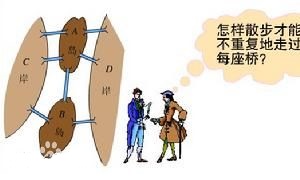
能否走过这样的七座桥，并且每桥只走一次？瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡七桥问题，并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。

你的任务是：对于给定的一组无向图数据，判断其是否成其为欧拉图？

Input

连续T组数据输入，每组数据第一行给出两个正整数，分别表示结点数目N(1 < N <= 1000)和边数M；随后M行对应M条边，每行给出两个正整数，分别表示该边连通的两个结点的编号，结点从1～N编号。 

Output

若为欧拉图输出1，否则输出0。

Example Input

1
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

Example Output

1

Hint

如果无向图连通并且所有结点的度都是偶数，则存在欧拉回路，否则不存在。 

 

DQE：

本题其实很简单不要想复杂了，注意题目Hint给的判定条件，执行一次深度优先搜索即可解决，祝大家顺利AC~

 

 #include <iostream>
 #include <cstdio>

 using namespace std;

 #define MVN 1010

 typedef struct AdjMatrix
 {
     int w;
     char *info;
 }AM;

 typedef struct MGraph
 {
     int vex[MVN];
     AM arc[MVN][MVN];
     int vexnum,arcnum;
 }MG;

 void creat(MG &G)
 {
     int i,j,k;
     for(k=;k<=G.vexnum;k++)
         G.vex[k]=k;
     for(k=;k<=G.arcnum;k++)
     {
         scanf("%d %d",&i,&j);
         G.arc[i][].w++;
         G.arc[j][].w++;
         G.arc[i][j].w=;
         G.arc[j][i].w=;
     }
 }

 int count;
 void DFS(MG G,bool *visited,int i)
 {
     visited[i]=true;
     count++;
     int k;
     for(k=;k<=G.vexnum;k++)
     {
         if(G.arc[i][k].w>&&visited[k]==false)
             DFS(G,visited,k);
     }
 }

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         MG G={};
         scanf("%d %d",&G.vexnum,&G.arcnum);
         creat(G);
         int k,f=;
         for(k=;k<=G.vexnum;k++)
         {
             if(G.arc[k][].w%!=)
             {
                 f=;
                 break;
             }
         }
         if(f)
         {
             printf("0\n");
             continue;
         }
         count=;
         bool visited[MVN]={false};
         DFS(G,visited,);
         if(count!=G.vexnum)
         {
             printf("0\n");
             continue;
         }
         printf("1\n");
     }
     return ;
 }

 /***************************************************
 User name: ***
 Result: Accepted
 Take time: 56ms
 Take Memory: 11588KB
 Submit time: 2016-11-09 21:56:24
 ****************************************************/