[杂题]URAL1822. Hugo II's War

看懂题意的请直接跳过下一坨！ 本人有表达障碍！

==========================================

题意： (题意真的很难很难懂啊！！！  去他娘的**)

有一个王国，王国里有一个国王(编号为1)，他有(编号为2~n) n-1个臣子(这些臣子并不全和他有直接关系)

然后呢 国王要去打架，但是只有当他的x%个及以上的直系下属(与他有直接关系的臣子)做好打架的准备了，他才能去打架

他的直系下属也有下属，也要其中x%及以上的下属做好打架准备了，那些直系下属才会开始准备打架...直到最后一层下属(也就是没有下属的那些人)他们会直接开始准备打架

当然 (除了国王)所有臣子准备打架都需要时间$t_i$；

有一个上限时间T 臣子们准备的总时间不能超过T

给的是n(包括国王 共n个人(国王加臣子))，T

接下来是编号2~n的臣子们的信息(1号是国王) $p_i$和$t_i$

$p_i$代表该臣子是   编号为pi的人  的下属

$t_i$代表该臣子      准备打架需要的时间

问的是： 不超过T的情况下，准备战斗的臣子要尽量多，求x的最大值

是不是看了这么大一坨还是不知道讲什么...

那么我们来看个案例：

6 3
1 2
2 2
2 1
1 2
1 4

n=6 T=3 就是1个国王 5个臣子 臣子们要在3单位时间内准备好打架
接着

2号：1 2
3号：2 2
4号：2 1
5号：1 2
6号：1 4

他们的关系图是这样的：

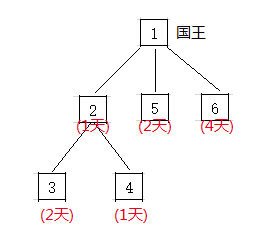
这些人中 3、4、5、6都是没有下属的 因此都可以直接开始准备打架

如果x是100，那么就是需要100%以上的下属完成准备，也就是当3、4完成2才能开始 ；当2、5、6完成1才能去打架

　　　　(3、4、5、6同时开始准备，3、4都完成过去了2天， 也就是第三天2可以开始准备(此时5也完成了)，然后过了4天2、5、6都完成，1就可以去打架了，所以x==100时总共用了4天)

如果x是50，那么就是需要50%以上的下属完成准备，也就是当3或4完成 2才能开始 ；当2、5、6中有2个人(ceil(3/2)=2)完成 1才能去打架

　　　　(3、4、5、6同时开始准备，第一天结束4完成，此时已经满足“2号的50%及以上的下属完成”，于是2开始准备，第2天结束，2准备完成，此时5也完成了，这样就满足了“1号的50%及以上的下属完成”，1就可以去打架了，所以x==50时总共用了2天)

题目的上限T==3也就是必须要在3天内完成准备 显然x==100的时候需要4天不满足，而x==50的时候需要2天，满足。

=================================================

呃 到这里 才讲完题目...

好了 那么怎么做呢？

我们先倒着思考，要是我们已知x(百分比)，继而来判断能不能满足“准备天数<=上限天数T”的条件 是不是就简单了很多呢，只要傻傻的相加就好了呢o(^▽^)o

好 那么我们就来枚举每一个百分比能不能满足条件 然后找个最大的！

浮点误差是$10^{-4}$那么0到100就总共$10^6$个情况，然后每个情况都要判断，最坏要加$10^4$次(n上限$10^4$)

那么就是O($10^4 \times 10^6$)，Time Limit：500ms

啊哦不够额 (￣▽￣)

那就二分呗~~上下限分别是0和100，结束的条件就是 fabs(l-r)<$10^{-4}$ 咯~~

然后就结束了...

然后一交WA *****

坑爹的居然要LL

时间上限T明明只有$10^6$，$t_i$明明只有100，$10^4$个100加起来也才$10^6$嘛！为什么要LL！

对啊！！写这么大一坨就是为了吐槽一个LL啊！

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const double eps=1e-;

 vector<LL> son[], tmp, tot;
 int a[];
 LL sum[];

 int main()
 {
     int n, t;
     scanf("%d%d", &n, &t);
     for(int i=;i<=n;i++)
     {
         int x;
         scanf("%d%d",&x,&a[i]);
         son[x].push_back(i);
     }
     a[]=;
     double l=, r=, ans;
     while(fabs(l-r)>=eps)
     {
         double m=(l+r)/2.0;
         memset(sum, -, sizeof(sum));
         tmp.clear();
         tmp.push_back();
         while(!tmp.empty())
         {
             int p=tmp[tmp.size()-];
             if(!son[p].size())
                 sum[p]=a[p], tmp.pop_back();
             else
             {
                 if(sum[son[p][]]==-)
                 {
                     for(int i=;i<son[p].size();i++)
                         tmp.push_back(son[p][i]);
                     continue;
                 }
                 tot.clear();
                 for(int i=;i<son[p].size();i++)
                     tot.push_back(sum[son[p][i]]);
                 sort(tot.begin(), tot.end());
                 int pp;
                 for(int i=;i<son[p].size();i++)
                     if((i+)*100.0/son[p].size()>=m)
                     {
                         pp=i;
                         break;
                     }
                 sum[p]=tot[pp]+(LL)a[p];
                 tmp.pop_back();
             }
         }
         if(sum[]<=t)
             ans=m, l=m;
         else
             r=m;
     }
     printf("%.7lf\n", ans);
     return ;
 }

URAL 1822