吴恩达机器学习笔记（十一） —— Large Scale Machine Learning

主要内容：

一.Batch gradient descent

二.Stochastic gradient descent

三.Mini-batch gradient descent

四.Online learning

五.Map-reduce and data parallelism

一.Batch gradient descent

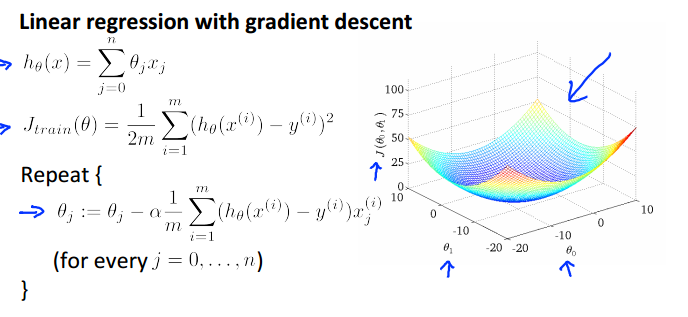
batch gradient descent即在损失函数对θ求偏导时，用上了所有的训练集数据（假设有m个数据，且m不太大）。这种梯度下降方法也是我们之前一直使用的。

如线性回归的batch gradient descent：

二.Stochastic gradient descent0

当数据集的规模m不太大时，利用batch gradient descent可以很好地解决问题；但是当m很大时，如 m = 100,000,000 时，如果在求偏导的时候，都利用上这100,000,000个数据，那么一次的迭代所耗的时间都是无法接受的。既然如此，就在求偏导的时候，只利用一个数据，但每一次迭代都利用上所有的数据。详情如下：

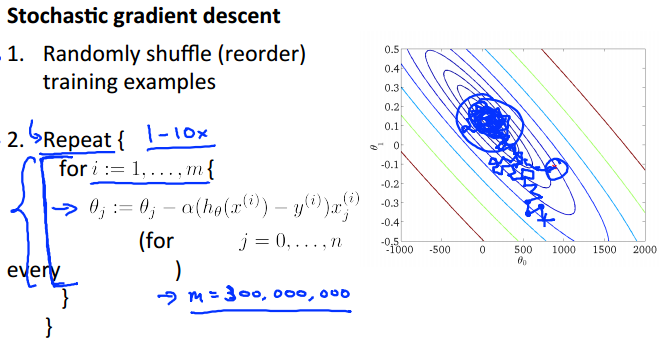
相当于把数据集抽到外面单独作为一层循环。

迭代效果：在迭代的过程中，由于求偏导时只用到了一个数据，所以很容易导致方向走偏。因而轨迹是迂回曲折的，且最终也不会收敛，而是在收敛点的附近一直徘徊。

那么，如何检测stochastic gradient descent的收敛情况？

对于batch gradient descent，我么可以画出损失函数随每一次迭代的变化情况。而对于stochastic gradient descent，我们可以在经过若干次迭代之后（如1000次后），求出这若干次迭代的平均损失值，并画图进行观察收敛情况。

优化：可知stochastic gradient descent在靠近最优点的时候，依然“大踏步”地徘徊，为了更加接近最优点（提高精度），我们可以：在每一次迭代靠近最优点的时候，都降低其学习率，即步长。这样，在越靠近最优点的时候，走的步伐就越细了，自然能更加接近最优点：

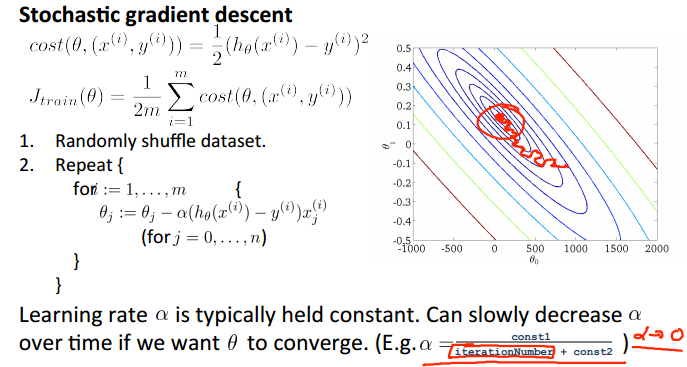
三.Mini-batch gradient descent

在求损失函数对θ求偏导时，batch gradient descent用上了所有的数据，而stochastic gradient descent则只利用了一个数据。可知，这两种做法都属于极端情况：batch gradient descent的轨迹是“心无旁骛，一直往最优点靠近”，而stochastic gradient descent是“像醉汉一样跌跌撞撞地往最优点靠近，且最后一直徘徊于最优点附近”。为了平衡这两种情况，我们可以采取这种的方法：求偏导的时候，即不用上所有数据，也不只是用一个数据，而是用一个子集的数据（子集的大小为b，假设b为10）。具体如下：

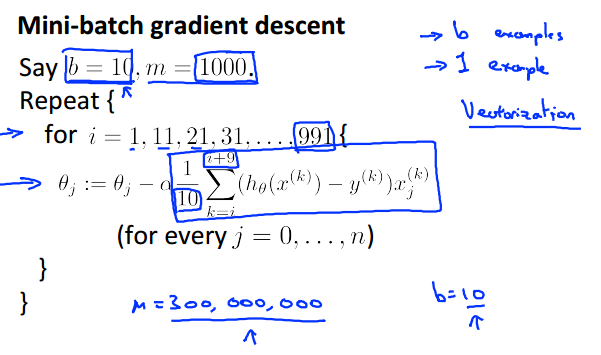
四.Online learning

很多时候，数据并不是一下子就能够收集完的，或者庞大的数据量只能慢慢地收集，如某一网站的一些链接的被点击次数等，都需要时间的积累。这时，就要用上在线学习了。

一下是两个在线学习的例子：

五.Map-reduce and data parallelism

当数据量很大时，我们可以将计算任务分配到多台计算机上（假如一台电脑有多个CPU，还可以是一台计算机上的多CPU分布式计算），然后再汇总计算结果，即所谓的分布式计算。

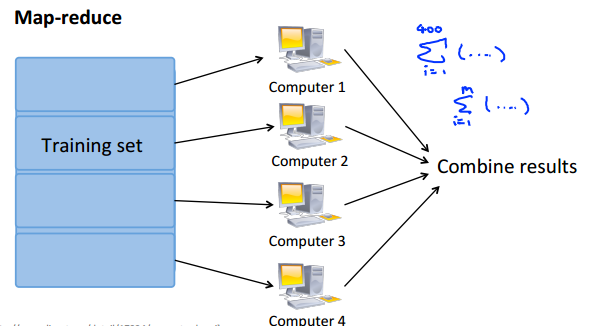
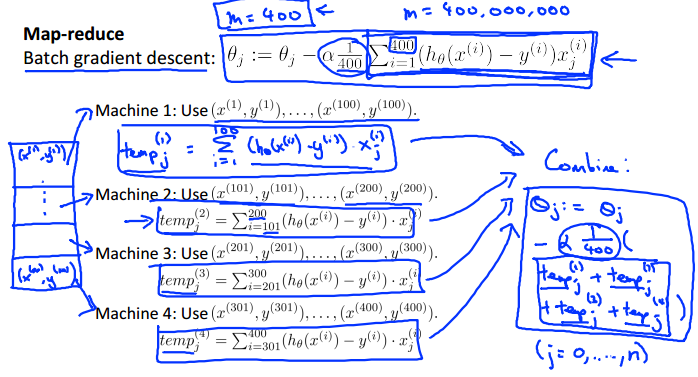
如可以将梯度下降求偏导的计算分布到赌台计算机上，然后汇总：