Applied Nonparametric Statistics-lec4

Ref:

https://onlinecourses.science.psu.edu/stat464/print/book/export/html/5

---

Two sample test

• 直接使用R的t-test

t.test(n, t, alternative="two.sided", var.equal=T)

• permutation test

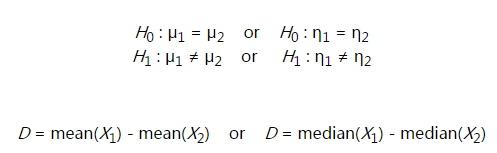
当我们判断两个样本的均值或者中值是否相等时，如果样本数量足够大，可以使用t-test。

但是，当两个样本的数量都很小时，它们的分布可能是有偏的，所以考虑permutation test。

原理：假设样本X1有m个数据，均值为mean(X1)；X2有n个数据，均值为mean(X2)。定义：D_obs=mean(X1)-mean(X2)

那么我们可以把m+n个数据放在一起，从中挑m个放到X1里，剩下的放到X2中。这样挑的方法共有k种：

计算D_i=mean(X1)-mean(X2) for i = 1...k

这样再与α比较，就可以判断要不要拒绝原假设。

当然，不止可以比较均值和中值，还可以比较trimmed mean.这三种方法的选择标准是：

数据接近正态分布，使用均值的差；

数据分布对称，但有离群值，使用trimmed mean（去掉极端值）的差；

数据分布不对称，使用中值的差。

那么，当m+n比较大时，遍历所有的D_i(i=1...k)就变成一件很耗时的事情。因此，我们希望可以估计这个p值，而不是计数然后计算。

同时，当k很大时，如果我们指定一个遍历次数，如999，那么这样计算出的p值和真实的p值之间的误差是很小的，因此，我们通过

指定k值，来减少耗时。其他步骤与前面一直，只是循环的次数是指定的而已。

• Wilcoxon Rank Sum Test

两样本非参数检验。我们首先将两个样本的数据合在一起，进行排序。然后计算样本1的rank的和，使用上面的方法，做permutation

当然，也可以使用样本2的rank sum。

另外，如果m和n小的话，可以使用表格。对于相等的数，排序时，我们使用均值。

此处参考University of Auckland的讲义：

• 相比t-test，Wilcoxon test对离群值更不敏感；
• Wilcoxon test更适合于检查两个样本分布的位置（图上可以用均值，中值描述），而非形状等其他方面的区别；
• Mann-Whitney test与Wilcoxon是等价的，虽然test statistic不一样。

不管原理的话，直接用R就好了啊～

wilcox.test(m, w, alternative="greater", exact=T)