【Java】 剑指offer(9) 斐波那契数列及青蛙跳台阶问题

 本文参考自《剑指offer》一书，代码采用Java语言。

更多：《剑指Offer》Java实现合集  

题目

　　写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。

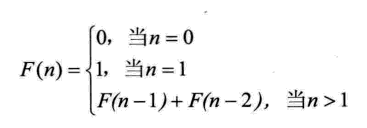
思路

　　如果直接写递归函数，由于会出现很多重复计算，效率非常底，不采用。

　　要避免重复计算，采用从下往上计算，可以把计算过了的保存起来，下次要计算时就不必重复计算了：先由f(0)和f(1)计算f(2)，再由f(1)和f(2)计算f(3)……以此类推就行了，计算第n个时，只要保存第n-1和第n-2项就可以了。

测试用例

　　1.功能测试（3，5，8等）

　　2.边界值测试（0，1，2等）

　　3.性能测试（50，100等）

　　4.特殊（负数）

完整Java代码

（含测试代码）

/**
 *
 * @Description 斐波那契数列
 *
 * @author yongh
 * @date 2018年9月13日 下午7:19:36
 */

// 题目：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。

public class Fibonacci {
	public long Fib(long n) {
		if(n<0)
			throw new RuntimeException("下标错误，应从0开始！");
		if (n == 0)
			return 0;
		if (n == 1)
			return 1;
		long prePre = 0;
		long pre = 1;
		long result = 1;
		for (long i = 2; i <= n; i++) {
			result = prePre + pre;
			prePre = pre;
			pre = result;
		}
		return result;
	}

	//附：缩略版（考虑到代码的可读性，其实还是上面的方法比较好）
	public long Fib2(long n) {
		if(n<0)
			throw new RuntimeException("下标错误，应从0开始！");
		if (n == 0)
			return 0;
		if (n == 1)
			return 1;
		long pre = 0;
		long result = 1;
		for (long i = 2; i <= n; i++) {
			result += pre;
			pre = result - pre;
		}
		return result;
	}

	public static void main(String[] args) {
		Fibonacci demo = new Fibonacci();
		System.out.println(demo.Fib(0));
		System.out.println(demo.Fib(1));
		System.out.println(demo.Fib(2));
		System.out.println(demo.Fib(8));
		System.out.println(demo.Fib(50));
		System.out.println(demo.Fib(100));
		System.out.println(demo.Fib(-5));
	}
}

　　

Exception in thread "main" java.lang.RuntimeException: 下标错误，应从0开始！

Fibonacci

　　 时间复杂度：O(n)

拓展

时间复杂度为O(longn)的解法

　　斐波那契数列有以下公式（可由数学归纳法推导得到）：

　　

　　由上式可知，求f(n)，只需要对矩阵求(n-1)次方即可，但此时时间复杂度仍为O(n)。利用乘方的性质

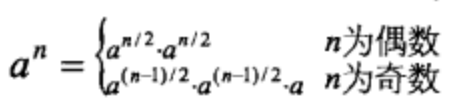
　　利用递归的思路计算乘方，即可将时间复杂度降低为O(longn)。这里给出对乘方函数的递归代码（引用）：

Matrix2By2 MatrixPower(unsigned int n)
{
    assert(n > 0);

    Matrix2By2 matrix;
    if(n == 1)
    {
        matrix = Matrix2By2(1, 1, 1, 0);
    }
    else if(n % 2 == 0)
    {
        matrix = MatrixPower(n / 2);
        matrix = MatrixMultiply(matrix, matrix);
    }
    else if(n % 2 == 1)
    {
        matrix = MatrixPower((n - 1) / 2);
        matrix = MatrixMultiply(matrix, matrix);
        matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0));
    }

    return matrix;
}

　　

青蛙跳台阶问题

　题目1：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　将跳法总数记为f(n)，可以知道f(1)=1，f(2)=2。当n>2时，第一次跳1级的话，还有f(n-1)种跳法；第一次跳2级的话，还有f(n-2)种跳法，所以可以推得f(n)=f(n-1)+f(n-2)，即为斐波那契数列。

　题目2：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　解法1：

　　当n=1时，f(1)=1。

　　当n大于1时，归纳总结可知：跳上n级台阶，第一次跳1级的话，有f(n-1)种方法；第一次跳2级的话，有f(n-2)种方法……第一次跳n-1级的话，有f(1)种方法；直接跳n级的话，有1种方法，所以可以得到如下公式：

　　f(n) = f(n-1)+f(n-2)+......f(1)+1　　（n≥2）

　　f(n-1) = f(n-2)+f(n-3)+.....f(1)+1　　（n>2）

　　由上面两式相减可得，f(n)-f(n-1)=f(n-1)，即f(n) = 2*f(n-1)  (n>2)

　　最终结合f(1)和f(2)，可以推得：f(n)=2^(n-1)

　　解法2：

　　假设跳到第n级总共需要k次，说明要在中间n-1级台阶中选出任意k-1个台阶，即C(n-1,k-1)种方法。

　　所以：跳1次就跳上n级台阶，需要C(n-1,0)种方法；跳2次需要C(n-1,1)种方法……跳n次需要C(n-1,n-1)种方法

　　总共需要跳C(n-1,0)+C(n-1,1)+C(n-1,2)+……C(n-1,n-1)=2^(n-1)种方法。

　　解法3：

　　除了必须到达最后一级台阶，第1级到第n-1级台阶都可以有选择的跳，也就是说对于这n-1个台阶来说，每个台阶都有跳上和不跳上2种情况，所以一共有2^(n-1)种方法。

矩形覆盖问题

　题目：用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

　　当n = 1时，有一种方法。

　　当n = 2时，有两种方法。

　　当n >= 3时，和斐波那契数列类似。第一步竖着放，有f(n-1)种方法；第一步横着放，有f(n-2)种方法。所以f(n)=f(n-1)+f(n-2)。

收获

　　1.求n次方时，可以利用递归来降低时间复杂度

　　2.当遇到涉及n的问题时（类似青蛙跳台阶问题），不要紧张，可以进行归纳分析，特别注意f(n)与f(n-1)、f(n-2)等的关联，从而找出规律，进行合理建模。

　　3.return (int)Math.pow(2,target-1);

　　　　1) 转int类型

　　　　2）pow不是power

更多：《剑指Offer》Java实现合集