最近公共祖先问题（LCA）的几种实现方式

LCA也是很经典的内容了，我这个蒟蒻居然今天才开始弄QAQ

我太弱啦！

照例先上定义——————转自维基百科

在图论和计算机科学中，最近公共祖先是指在一个树或者有向无环图中同时拥有v和w作为后代的最深的节点。在这里，我们定义一个节点也是其自己的后代，因此如果v是w的后代，那么w就是v和w的最近公共祖先。

最近公共祖先是两个节点所有公共祖先中离根节点最远的，计算最近公共祖先和根节点的长度往往是有用的。比如为了计算树中两个节点v和w之间的距离，可以使用以下方法：分别计算由v到根节点和w到根节点的距离，两者之和减去最近公共祖先到根节点的距离的两倍即可得到v到w的距离。

下面蒟蒻就尝试总结几种求LCA的方式

1.倍增求LCA，优点：易于实现，理解难度不大

复杂度：预处理复杂度O(NlogN)，查询复杂度O(logN)

2.ST表（RMQ）求lca，优点....可能是对于rmq学的好的人更容易理解？原谅蒟蒻rmq学的太烂qwq

复杂度：预处理O(NlogN)带一个常数，查询同样是O(logN)

3.tarjan求lca，优点是易于理解外加速度飞快，但他是离线算法，因此不适用于强制在线的题目

复杂度：O(N+M)

4.树链剖分求lca.....优点是所需空间很小...跑的也是飞快...

复杂度期望O(NlogN)，但实际常数极小..理论上是最优的lca解法，

然而我不会啊orzzzzzzzzz

那么这篇博客主要就写一写倍增，基本能解决所有问题了

题目：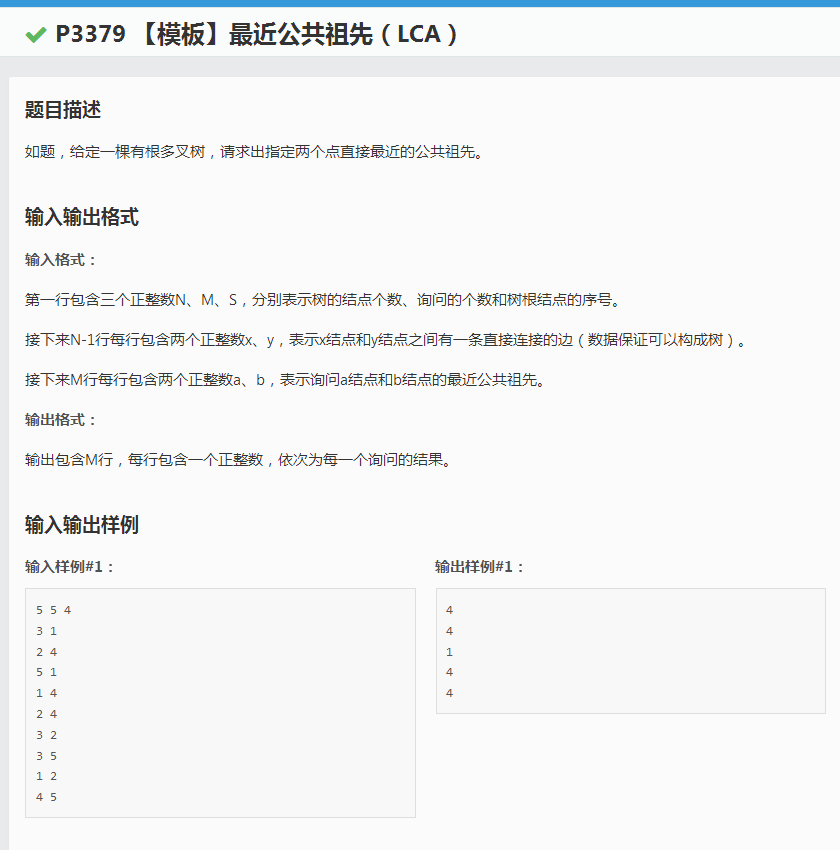

利用的是倍增 参考了yycc神犇的代码，%%%%%

#pragma GCC optimize("O2")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<limits.h>
#include<ctime>
#define N 100001
typedef long long ll;
const int inf=0x3fffffff;
const int maxn=2017;
using namespace std;
inline int read()
{
    int f=1,x=0;char ch=getchar();
    while(ch>'9'|ch<'0')
    {
        if(ch=='-')
        f=-1;
        ch=getchar();
    }
    while(ch<='9'&&ch>='0')
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return f*x;
}
struct tsdl{
    int w,to,next;
} edge[N*4];
int tot=0,head[500005],dp[500005][25],n,m,root,dep[500005];
void add(int ui,int vi)
{
    edge[tot].next=head[ui];
    edge[tot].to=vi;
    head[ui]=tot++;
}

bool vis[500005];
void dfs(int x)
{
    vis[x]=1;
    for(int i=1;i<=20;i++)
    {
        if(dep[x]<(1<<i))break;//如果肯定跳不到，那么后面更不可能跳到，直接跳出
        dp[x][i]=dp[dp[x][i-1]][i-1];//这句话是整个倍增算法的核心,也就是x的1<<i-1距离的祖先的1<<i-1距离的祖先是x的1<<i距离的祖先
    }
    for(int i=head[x];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(vis[v])continue;
        dep[v]=dep[x]+1,dp[v][0]=x;//V的直接祖先是x
        dfs(v);
    }
}
int lca(int x,int y)
{
    if(dep[x]<dep[y])swap(x,y);
    for(int i=20;i>=0;i--)
    if(dep[y]<=dep[dp[x][i]])//如果可以跳，先跳一次
    x=dp[x][i];
    if(x==y)return x;//特判直接跳出
    for(int i=20;i>=0;i--)
    {
        if(dp[x][i]!=dp[y][i])//只有在跳之后不同才跳
        x=dp[x][i],y=dp[y][i];
    }
    if(x==y)return x;
    if(dp[x][0]==0)return root;
    return dp[x][0];//此时x的直接祖先即为答案
}
int main()
{
    n=read(),m=read(),root=read();
    memset(head,-1,sizeof(head));
    for(int i=1;i<n;i++)
    {
        int x=read(),y=read();
        add(x,y),add(y,x);
    }
    dfs(root);
    while(m--)
    {
        int x=read(),y=read();
        printf("%d\n",lca(x,y));
    }
}