字符串----hiho字符串(尺取法)

　　

　　注意：这道题的解法和最短摘要一样，都是采用尺取法解决问题，注意这儿题目要求恰好包含，也就是说这个hiho字符串必须包含2个'h'、1个'i'和1个'o'。一个不能多，一个也不能少。

 import java.util.Scanner;

 public class HihoStr {
     public static void main(String[] args) {
         Scanner scanner = new Scanner(System.in);
         String str = scanner.nextLine();
         char[]w = str.toCharArray();
         sovel(w);
     }

     private static void sovel(char[] w) {
         int min = Integer.MAX_VALUE;
         int j = -1;
         for (int i = 0; i < w.length; i++) {
             char c = w[i];
             if(check(c)){ //i停下
                 if (j==-1) {  // j的第一次定位
                     j = i+1;
                 }
                 while(j<w.length){
                     char c2 = w[j];
                     if (check(c2)&&containsAll(w,i,j)) {  // 全部囊括
                         if (check(w,i,j)&&j-i+1<min) { // 更新min
                             min = j-i+1;
                         }
                         break;  // j停下
                     }
                     j++;
                 }
             }
         }
         System.out.println(min==Integer.MAX_VALUE?-1:min);
     }

     private static boolean containsAll(char[] w, int i, int j) {
         int c1=0,c2=0,c3=0;
         for (int k = i; k <= j; k++) {
             if(w[k]=='h') c1++;
             if(w[k]=='i') c2++;
             if(w[k]=='o') c3++;
         }
         return c1>=2&&c2>=1&&c3>=1;
     }

     /**
      * 检查字符序列是否恰好包含2个h，一个i，一个o
      * @param w
      * @param i
      * @param j
      * @return
      */
     private static boolean check(char[] w, int i, int j) {
         int c1=0,c2=0,c3=0;
         for (int k = i; k <= j; k++) {
             if(w[k]=='h') c1++;
             if(w[k]=='i') c2++;
             if(w[k]=='o') c3++;
         }
         return c1==2&&c2==1&&c3==1;
     }

     private static boolean check(char c) {
         return c=='h'||c=='i'||c=='o';
     }

 }

　　结果：

　　　　

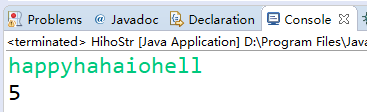
　　尺取法的模型：根据区间的特征交替推进左右端点求解问题，其高效的原因在于避免了大量的无效枚举，其区间枚举都是根据区间特征有方向的枚举，如果胡乱使用尺取法的话会使得枚举量减少，因而很大可能会错误，所以关键的一步是进行问题的分析！下面分析一下尺取法的过程：