留恋 nyoj 854

留恋

时间限制：1000 ms  |  内存限制：65535 KB

难度：2

 

描述

大家都知道，高中的时候，座位基本都是固定的，但是对于视力不好却又坐在后面的人是很不公平的。

念情的高中班主任安哥是个非常好的班主任，他为每个人着想，制定了一种的换位规则，每周执行一次：

每次都向右下角移动一个位置（即本周坐（0，1），则下周坐（1,2））

若已移动到边上，则返回顶部（即在行数为3的情况下，本周在（2，n），则下周在（0，n+1），列同）

现在念情想知道，如果教室有（n*m）个座位，他能不能把所有的座位都坐一次呢？（假设念情读高中的时间无限）

 

输入

第一行一个整数N表示N组测试数据
接下来N行每行两个整数n,m表示教室的座位
1<n<10000
1<m<10000

输出

若念情能够把座位都坐一边，则输出Possible，否则输出Impossible

样例输入

3
2 3
2 2
3 6

样例输出

Possible
Impossible
Impossible

方法一：利用最小公因数

//最小公因数
#include<iostream>
using namespace std;
int gcd(int a, int b) ;
int main() {
  int t;
  cin >> t;
  while (t--) {
    int n, m;
    cin >> n >> m;
    if (gcd(n, m) == ) {
      cout << "Possible" << endl;
    } else {
      cout << "Impossible" << endl;
    }
  }
}
int gcd(int a, int b) {
  if (a%b == ) return b;
  return gcd(b,a%b);
}

方法二：

分析图：

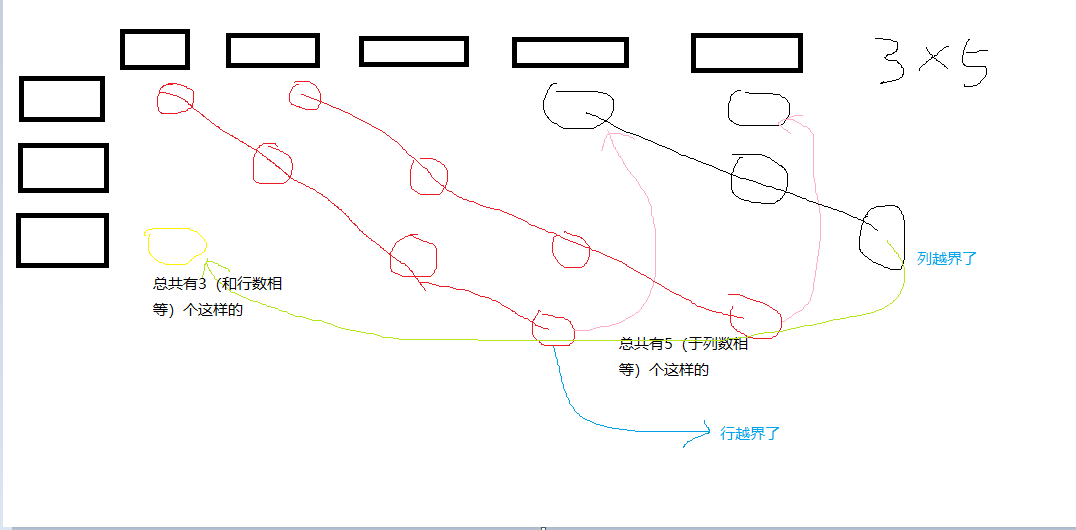
#include<iostream>
#include<cstring>
using namespace std;
const int N = ;
int col[N], row[N];
int main() {
  int t;
  cin >> t;
  while (t--) {
    int n, m;
    cin >> n >> m;
    int i , j, x, y;
    i = j = x = y = ;
    memset(col,,sizeof(col));
    memset(row,,sizeof(row));
    while (x <= n && y <= m) {
      if (n-i+ < m-j+) {j = j+ n-i+; i = n+; }//i 先到达底部   同时移动n-i+1 步
      else if (n-i+ > m-j+) {i = i +m-j+; j = m+;  }//j 先到达底部
      else { i = n+; j = m+;}//i、j 同时到达底部
      if (i > n) { //i 比n大时i必等于n+1
        i = ;
        if (j <= m) {
          if (col[j]) break;
          col[j] = ;
          y++;
        } else {//i 比m大时i必等于m+1  既要向左转
          col[] = ;
          y++;
        }
      }
      if (j > m) {//i 比m大时i必等于m+1
        j = ;
        if (i <= n) {
          if (row[i]) break;
          row[i] = ;
          x++;
        } else {//i 比n大时i必等于n+1  既要向上转
          row[] = ;
          x++;
        }
      }
    }
    if (x == n+ && y == m+) {//每一个座位都做遍了
      cout << "Possible" << endl;
    } else {
      cout << "Impossible" << endl;
    }
  }
}