[JLOI2015]骗我呢

Tags：题解

TAG：数学，DP

题意

骗你呢

求满足以下条件的$n*m$的矩阵的个数对$10^9+7$取模

对于矩阵中的第$i$行第$j$列的元素$x_{i,j}$都有

$x_{i,j}<x_{i,j+1}$
$x_{i,j}<x_{i-1,j+1}$
$0\le x_{i,j}\le m$

题解

Part 0 前言

不会做啊！（杠了四五个小时！）

谢两位dalao：blog1、blog2

以下图片均来自于此篇文章：http://www.cnblogs.com/coco-night/p/9552677.html，如有冒犯请与我联系，谢谢！

Part 1 朴素DP

首先发现一个很好的性质：

每行是递增的并且一行$m$个元素，取值只能在$[0,m]$中选

那么必然该行至多有一个位置与后一个位置相差2，其余的都只相差1

由此可以列出一个简单的$DP$：

$dp[i][j]$表示第$i$行没有出现过的数是$j$的方案数

$dp[i][j]=\sum_{k=0}^{j+1}dp[i-1][k]$

至于上界为什么是$j+1$可以手动模拟一下，假设这行$j$没有出现过，上一行试一试$j-1$、$j$、$j+1$、$j+2$，发现大于$j+1$的就不合法了

略微优化一下就变成了$dp[i][j]=dp[i-1][j+1]+dp[i][j-1]$

Part 2 转化为图形

发现这个$DP$像极了组合数公式，把它套用在坐标系里就是这个样子

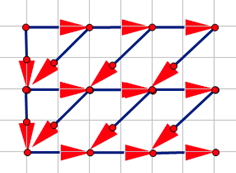
自上而下第$i$行，从左往右第$j$列的点就表示$dp[i][j]$，其指向的点就表示可以转移

这样仍然不太好处理，我们继续转化：

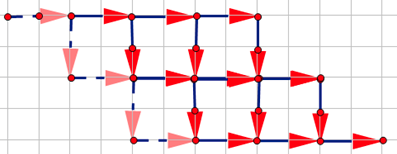
还是不好看，给它对称一下：

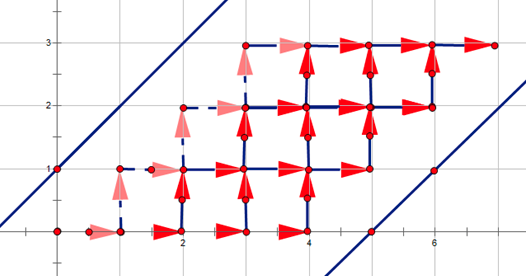
Part 3 挖掘组合意义

这么一看，不就是从原点出发，只能向右或向上走，不接触直线A,B，到达点(n+m+1,n)的路径条数吗！

直线$A:y=x+1$，直线$B:y=x-(m+2)$

Part 4 计算

这种格路数计算（如两双手）都可以考虑采用容斥计数

不考虑其他限制，原点到$x,y$的方案数是$C_{x+y}^x$

考虑不合法方案是什么：如依次经过$AABBAAAABB$

把它缩一下：$ABAB$

可以发现不合法方案要么以$A$开头要么以$B$开头

表示为首次跨越的直线是$A$还是$B$

所以：答案=总方案数 - A开头的方案数 - B开头的方案数

$x=n+m+1,y=n$，把$(x,y)$沿$A$对称得到$(x',y')=(y-1,x+1)$

每条从$(0,0)$到$(x',y')$的路径都依次对应一条以A结尾或者以AB结尾的路径！

如图：（这个图是我自己画的！）

上面是一条以$A$结尾的路径

上面是一条以$AB$结尾的路径

所以，总共的不合法方案是

A
B
AB
BA
ABA
BAB
ABAB
BABA
...

为了减去以$A$开头的方案，需要减去以A,AB结尾的方案，加上以BA,BAB结尾的方案，减去....

那么实现方式是：把(x,y)沿A翻折，减去答案；将翻折过的点沿B翻着，加上答案；再沿A翻折...

同理计算以$B$开头的方案，就是先沿$B$折就好了

具体细节的话沿着$A$折是$(x,y)->(y-1,x+1)$，沿着$B$折是$(x,y)->(y+(m+2),x-(m+2))$

复杂度是O(n)的，复杂度瓶颈为预处理阶乘，至于计算每次是像跳棋一样，复杂度为$O(logn)$

完美解决本题！

代码

#include<iostream>

using namespace std;

const int P=1e9+7,N=3e6+10;

int n,m,up,inv[N],jc[N],inj[N];

int Calc(int x,int y) {return (x<0||y<0)?0:1ll*jc[x+y]*inj[x]%P*inj[y]%P;}

void flip1(int &x,int &y) {swap(x,y);x--;y++;}

void flip2(int &x,int &y) {swap(x,y);x+=m+2;y-=m+2;}

void add(int &x,int y) {x+=y;if(x>=P) x-=P;}

int main()

{

	cin>>n>>m;inv[0]=inv[1]=jc[0]=inj[0]=1;up=max(n,m)*3+1;

	for(int i=2;i<=up;i++) inv[i]=(P-1ll*P/i*inv[P%i]%P)%P;

	for(int i=1;i<=up;i++) jc[i]=1ll*jc[i-1]*i%P,inj[i]=1ll*inj[i-1]*inv[i]%P;

	int x=n+m+1,y=n,ans=Calc(x,y);

	while(x>=0&&y>=0)

	{

		flip1(x,y);add(ans,P-Calc(x,y));

		flip2(x,y);add(ans,Calc(x,y));

	}

	x=n+m+1,y=n;

	while(x>=0&&y>=0)

	{

		flip2(x,y);add(ans,P-Calc(x,y));

		flip1(x,y);add(ans,Calc(x,y));

	}

	return cout<<ans<<endl,0;

}