隐马尔可夫（HMM）模型

隐马尔可夫（HMM）模型

　　隐马尔可夫模型，是一种概率图模型，一种著名的有向图模型，一种判别式模型。主要用于时许数据建模，在语音识别、自然语言处理等领域广泛应用。

　　概率图模型分为两类，一类：使用有向无环图表示变量间的依赖关系，称为有向图模型或者贝叶斯网；第二类：使用无向图表示变量间的依赖关系，称为无向图模型或者马尔可夫网。

　　判别式模型：考虑条件分布P(Y, R | O)，生成式模型：考虑联合分布P(Y, R, O)

HMM三个假设

• 当前观测值只由当前隐藏状态决定
• 当前隐藏状态由前一个隐藏状态决定
• 隐藏状态之间转移概率不随时间改变

随机过程中某一时刻的状态s_t的概率分布为：

p(s_t|s_t-1,s_t-2,...,s₀)=p(s_t|s_t-1)

即：t 时刻的状态仅依赖于 t-1 时刻的状态，与其余状态无关，这就是所谓的“马尔可夫链”

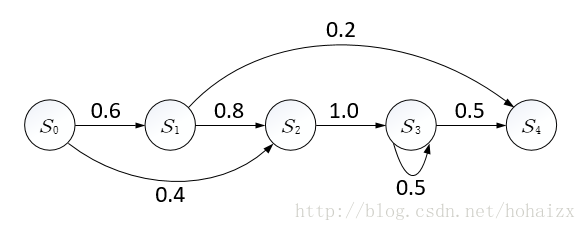
在马尔可夫链中，每一圆圈代表相应时刻的状态，有向边代表可能的状态转移，权重表示状态转移的概率

HMM模型结构图

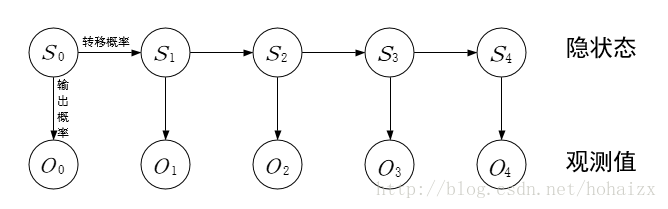
HMM模型五元组

HMM模型可以用五元组(O, S, A, B, π)表示。其中

• O: {o₀, o₁, ..., o_n} 表示观测系列，是系统的外在可观测变量。
• S: {s₀, s₁, ..., s_n} 表示隐状态序列，是导致系统外在表现变化的内因。
• A: {a_ij = p(s_j | s_i)} 表示状态转移概率。
• B: {b_ij = p(o_j | s_i)} 表示输出概率，又称发射概率
• π: {π₀, π₁, ..., π_m} 表示初始状态概率。

HMM三类问题

根据以上HMM模型五元组表示，我们可以归纳出HMM模型解决的三类主要问题。

一、评估问题

已知：状态转移矩阵 A， 初始状态概率 π，输出矩阵 B，观测序列

求：求该观测序列的可能性

解决算法：向前（forward）算法或者向后（backward）算法

二、解码问题

已知：状态转移矩阵A，初始状态概率 π，输出矩阵B，观测序列

求：最有可能产生该观测序列的隐藏状态序列

解决算法：维特比（Viterbi）算法，一种动态规划算法

三、学习问题

已知：很多观测序列

求：估计HMM模型参数的可能取值

解决算法：鲍姆韦尔奇（Baum-Welch）算法