批量梯度下降(BGD)、随机梯度下降(SGD)以及小批量梯度下降(MBGD)的理解

  梯度下降法作为机器学习中较常使用的优化算法，其有着三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度学习中进行模型的训练。接下来，我们将对这三种不同的梯度下降法进行理解。
  为了便于理解，这里我们将使用只含有一个特征的线性回归来展开。此时线性回归的假设函数为：
\[ h_{\theta} (x^{(i)})=\theta_1 x^{(i)}+\theta_0 \]
  其中 $ i=1,2,...,m $ 表示样本数。
  对应的目标函数（代价函数）即为：
\[ J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 \]
  下图为 $ J(\theta_0,\theta_1) $ 与参数 $ \theta_0,\theta_1 $ 的关系的图：

---

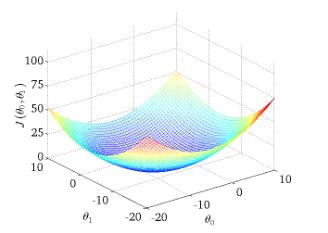
1、批量梯度下降（Batch Gradient Descent，BGD）

  批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。从数学上理解如下：
  （1）对目标函数求偏导：
\[ \frac{\Delta J(\theta_0,\theta_1)}{\Delta \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} \]
  其中 $ i=1,2,...,m $ 表示样本数， $ j = 0,1 $ 表示特征数，这里我们使用了偏置项 $ x_0^{(i)} = 1 $ 。
  （2）每次迭代对参数进行更新：
\[ \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} \]
  注意这里更新时存在一个求和函数，即为对所有样本进行计算处理，可与下文SGD法进行比较。
  伪代码形式为：
  repeat{
       $ \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} $
      (for j =0,1)
  }

  优点：
  （1）一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
  （2）由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。
  缺点：
  （1）当样本数目 $ m $ 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
  从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：

---

2、随机梯度下降（Stochastic Gradient Descent，SGD）

  随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
  对于一个样本的目标函数为：
\[ J^{(i)}(\theta_0,\theta_1) = \frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2 \]
  （1）对目标函数求偏导：
\[ \frac{\Delta J^{(i)}(\theta_0,\theta_1)}{\theta_j} = (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j \]
  （2）参数更新：
\[ \theta_j := \theta_j - \alpha (h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_j \]
  注意，这里不再有求和符号
  伪代码形式为：
  repeat{
    for i=1,...,m{
       $ \theta_j := \theta_j -\alpha (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} $
      (for j =0,1)
    }
  }

  优点：
  （1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
  缺点：
  （1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
  （2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
  （3）不易于并行实现。

  解释一下为什么SGD收敛速度比BGD要快：
  答：这里我们假设有30W个样本，对于BGD而言，每次迭代需要计算30W个样本才能对参数进行一次更新，需要求得最小值可能需要多次迭代（假设这里是10）；而对于SGD，每次更新参数只需要一个样本，因此若使用这30W个样本进行参数更新，则参数会被更新（迭代）30W次，而这期间，SGD就能保证能够收敛到一个合适的最小值上了。也就是说，在收敛时，BGD计算了 $ 10 \times 30W $ 次，而SGD只计算了 $ 1 \times 30W $ 次。

  从迭代的次数上来看，SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下：

---

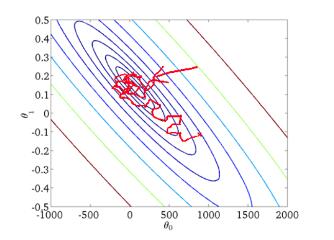
3、小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

  小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用 ** batch_size** 个样本来对参数进行更新。
  这里我们假设 $ batch_size = 10 $ ，样本数 $ m=1000 $ 。
  伪代码形式为：
  repeat{
    for i=1,11,21,31,...,991{
       $ \theta_j := \theta_j - \alpha \frac{1}{10} \sum_{k=i}^{(i+9)}(h_{\theta}(x^{(k)})-y^{(k)})x_j^{(k)} $
      (for j =0,1)
    }
  }

  优点：
  （1）通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
  （2）每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
  （3）可实现并行化。
  缺点：
  （1）batch_size的不当选择可能会带来一些问题。

  batcha_size的选择带来的影响：
  （1）在合理地范围内，增大batch_size的好处：
    a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
    c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
  （2）盲目增大batch_size的坏处：
    a. 内存利用率提高了，但是内存容量可能撑不住了。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
    c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

  下图显示了三种梯度下降算法的收敛过程：

---

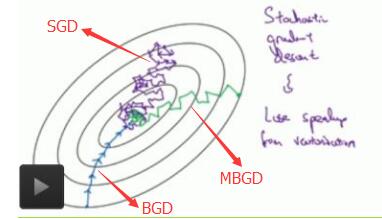
引用及参考：
[1] https://www.cnblogs.com/maybe2030/p/5089753.html
[2] https://zhuanlan.zhihu.com/p/37714263
[3] https://zhuanlan.zhihu.com/p/30891055
[4] https://www.zhihu.com/question/40892922/answer/231600231

写在最后：本文参考以上资料进行整合与总结，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9451903.html