9 Days 停课修炼题解集

xj4604 排序

\(n,k <= 1e5\).

先考虑二分出这个值，check 有多少段的平均值小于这个 mid，这个在之前的复活赛中是原题 T4，数形结合，$ \text{Average} = \frac{Sum_i-Sum_j}{i-j} $，可以把它看做一个两点间的斜率公式——每个位置把它搞到平面上的点对 \((i,Sum_i)\)，求有多少点对的斜率小于 mid。把它分成每个点的贡献——分别求一个点左侧有多少点能与它斜率小于等于 mid，过每个点作一条斜率为 mid 的直线，求出纵截距 \(-mid \times i + Sum_i\)，这就是一个二维偏序问题了，用归并排序就行。

考虑怎么优化掉一个 \(\log\)——不妨把每个点的这个截距式看做以 \(mid\)为变量的函数，可以得到这样的东西——

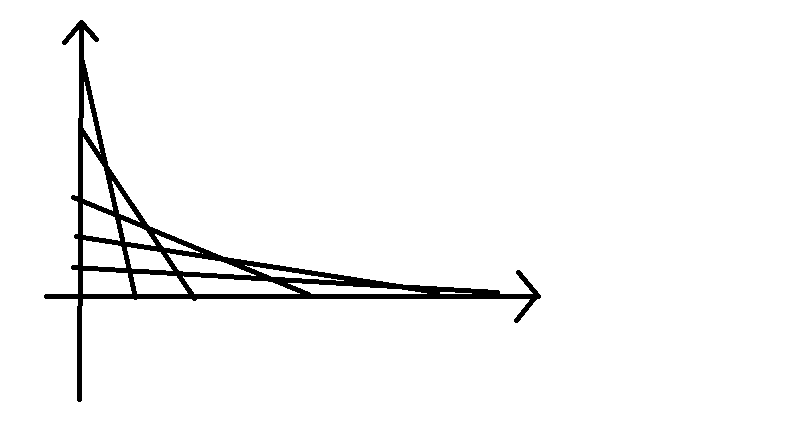
上面的每一个交点都代表一个区间的平均值，求横坐标第 k 大的交点—— k 不是很大，所以就可以这么求：从左到右扫，假设我们知道线段在当前横坐标、的按照纵坐标的排序的结果，那么下一个交点肯定由相邻的两条线段得到；然后我们再扫到下一个交点的横坐标，显然只有这两条线段的上下关系发生变化，交换一下就可以得出下一个序列......差不多就是这个意思，代码见 Peanut_Tang 学长的 代码。

xj4591 program

\(n,a,b <= 3e2\).

直接上状态：设 $f[i][j][k] $表示现在在枚举第 i 行字符串、枚举到了第 j 个位置、当前连续段长度为 k 的最小代价，于是可以得到转移方程：

\[f(i,j,k)=\left\{
\begin{aligned}
\min\{f(i,i-j,k')+(j-k)^2 \}\ (j \not= k)\\
\min\{f(i-1,b_i,k')+(j-b_i+a_i-a_{i-1})\} (j=k)
\end{aligned}
\right.\]

上面的方程是四次方的，下面的是三次方的，只要优化上面的就行了。展开之后用上斜率优化就行了。有的时候，状态的设置要清楚明确一点，分情况来写，就非常有利于分析。

xj4592 birthday

巧妙的构造题（数竞内鬼题）。

我们构造如下：

可以通过巧妙的递归来实现：

int f[maxn][maxn][maxn];

void dfs(int x, int y, int z, int dep)
{
    if (z <= 0) return;
    if (f[dep][x][y]) return;
    f[dep][x][y] = z;
    dfs(x - 1, y, z - 1, dep + 1);
    dfs(x, y - 1, z - 2, dep + 1);
    dfs(x, y + 1, z - 3, dep + 1);
    dfs(x + 1, y, z - 4, dep + 1);
}

int main()
{
    //vector<oper> v;
    int n;
    cin >> n;
    dfs(105, 105, n, 1);
    for (int i = 200; i; i--)
    {
        for (int j = 200; j; j--)
        {
            for (int k = 200; k; k--)
            {
                if (f[i][j][k])
                {
                    cout << j << " " << k << " " << f[i][j][k] << endl;
                }
            }
        }
    }
    return 0;
}

华灵「蝶妄想」 (butterfly)

又是一道构造题，有一个东西我们是知道的——若我们把第一行选上了，那么必然会破坏掉 \(\frac{1}{2}m\) 列。同理，最后一行、最后一列、第一列都不值得选上——若我们能构造出方案数与\(n\)、\(m\)呈系数为一的方法，那么当\(n \leq 4\)时肯定是必须这么做更优——于是我们可以得到一个答案为 \(n+m-4\) 的构造：

当\(n\)足够大时，这个是最优的，但是\(n=2\)和\(n=4\)要特判。

樱符「完全墨染的樱花」 (sakura)

\(n<=1e5,m<=5e5\).

显然这张图是一个仙人掌，先来考虑树的情况怎么做。

大胆的运用最大流最小割定理，两点之间的最大流就等于它们路径上的最小值。这个东西最难优化的地方在于求最小值，所以我们把边权从小到大依次加入，新加入的这条边就是它联通的两个连通块之间的点对的最大流的值。于是我们用并查集统计这一过程的贡献；具体来说，维护每个连通块的\(p^c\)之和与\(p^{c(n-1)}\)之和，每次合并的时候加上这条边的贡献就行了。

然后考虑仙人掌怎么做。由于环没有重叠，我们分成一个个环来讨论：可以发现把每个环上的最小的边去掉，并把它的容量加到这个环的其他边上，这个新的树的最小割和原来的最小割完全等价，在这棵树上按照原来的方法统计就行了，用树上差分更新权值就能保证复杂度。

正确性的证明：显然。

xj4584 随机游走

你从 A 出发，接下来的每一天，你会从 x 达到 (x+f(x))modM，问 N−1 天后你的位置，其中 f(x) 表示 x 十进制表示中最大的数码。

\(n<=1e6\)直接暴力、\(m<=1e6\)开个桶找循环节，这都简单。考虑怎么优化。

这是一道求值的题目，又推不出什么式子，所以只能考虑倍增。我们先把它增大到$

咕着咕着

幽曲「埋骨于弘川」 (buried)

跟上一题做法类似，也咕着吧。

燃烧的火焰 (flame)

\(\Theta(n2^k\log n)\)做法就比较显然，枚举k中每个点选还是不选，以这个点集为起点，跑一遍最短路就行了，看一下最短路最远的那个点的距离是否比原答案大。

事实上我们发现我们根本不用跑这么多次的最短路，我们只需要跑 \(k\)次最短路就可以了。形式化的，若当前枚举到的子集是\(T\)，则点\(x\)的最短路就是\(\max_{i\in T}\{dis_{i,x}\}\)。那我们要求的，就是

\[\sum_{T\in S}\{[\max_{i\in T}\{dis_{i,x}\}=ans]\}
\]

的子集T的个数。我们直接处理这个 \(k\) 显然过于困难。由于每个点的对答案的限制是分别独立的，所以单独看一下一个点的贡献：出发点们到它的距离有些小于答案，有些大于答案；当且仅当选出的出发点全部属于这个距离大于答案的点集时，它会不合法。所以我们开一个\(2^k\)的桶，每次把这个集合和它的子集全部删掉。如何快速删除子集呢？考虑离线下来一起处理。从大到小扫描桶的值域，当扫到一个删掉的集合时，枚举去掉它的哪一位，把这\(k\)个集合设为非法；否则 ans++。

这么做显然是不重不漏的，巧妙的不得了。

消失的序列 (stack)

喵喵喵啊！lzy: 对于栈的计数问题，有一种常见的数形结合方法：

图中，向右的一条边代表了一次入栈，向上的一条边代表了一次出栈；由于入栈和出栈序列已经定下来了，所以每条边的边权就已经定下来了，如图所示；一条从\((0,0)\)到\((n,n)\)路径对应了一种入栈和出栈的方式；我们要统计\(a\)数组的个数，其实每个\(a\)数组与\((0,0)\)到\((n,n)\)的路径也一一对应，因为根据出栈序列和路径可以还原出唯一且存在的入栈序列。现在考虑加上这个\(a_{pos}=x\)的限制，如图：

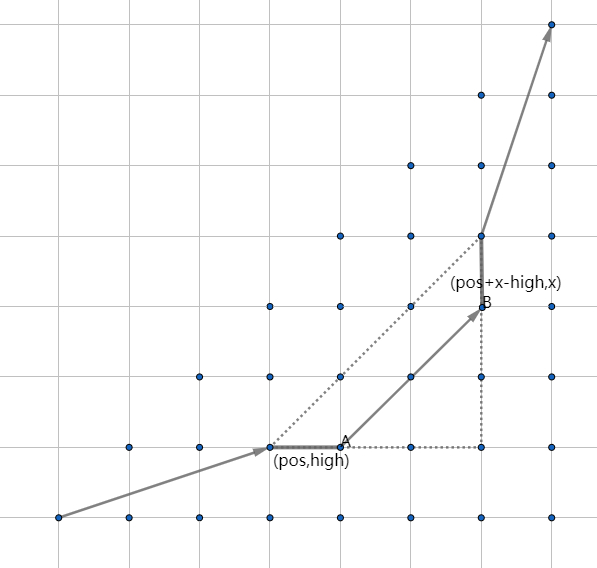
枚举\(pos\)位置的高度，由于出栈的限制，我们可以得出它必定经过上边的那个出栈序列；现在问题就转化为从\((0,0)\)到\((pos,high)\)再到那个再到\((n,n)\)的方案数的乘积。这个方案数怎么求呢？

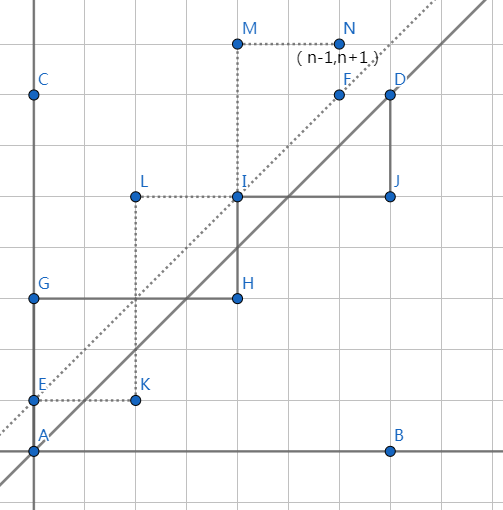
用总的方案数\(C_{2n}^n\)减去不合法的方案数。发现不合法的方案一定会经过\(y=x+1\)那条线，若把这些方案沿\(y=x+1\)翻转，于是它最后会到达点\((n-1,n+1)\)；我们大胆猜想：不合法的方案与从\((0,0)\)到\((n-1,n+1)\)的方案数一一对应，合法的方案数就是\(C_n=C_{2n}^n-C_{2n}^{n-1}\)。类似的，若三角形是\((n,m)\)，那么不合法就是从\((0,0)\)走到\((m-1,n+1)\)，合法方案数就是\(C_{n,m}=C_{n+m}^n-C_{n+m}^{n+1}\)，这个叫类卡特兰数。

另外，许多问题（如节点数是\(n\)的二叉树个数）可以通过\(O(n^2)\)的递推式$C_n=\sum_{j=0}^{n-1} C_j C_{n-j-1} $ 来证明答案是卡特兰数。具体右转 lzy 大佬的 Blog。