TCP 两次握手为什么无法阻止历史连接？

摘要：在两次握手的情况下，「被动发起方」没有中间状态给「主动发起方」来阻止历史连接，导致「被动发起方」可能建立一个历史连接，造成资源浪费。

本文分享自华为云社区《TCP 两次握手为什么无法阻止历史连接？》，作者：小林coding 。

两次握手的情况下，「被动发起方」在收到 SYN 报文后，就进入 ESTABLISHED 状态，意味着这时可以给对方发送数据给，但是「主动发」起方此时还没有进入 ESTABLISHED 状态，假设这次是历史连接，主动发起方判断到此次连接为历史连接，那么就会回 RST 报文来断开连接，而「被动发起方」在第一次握手的时候就进入 ESTABLISHED 状态，所以它可以发送数据的，但是它并不知道这个是历史连接，它只有在收到 RST 报文后，才会断开连接。

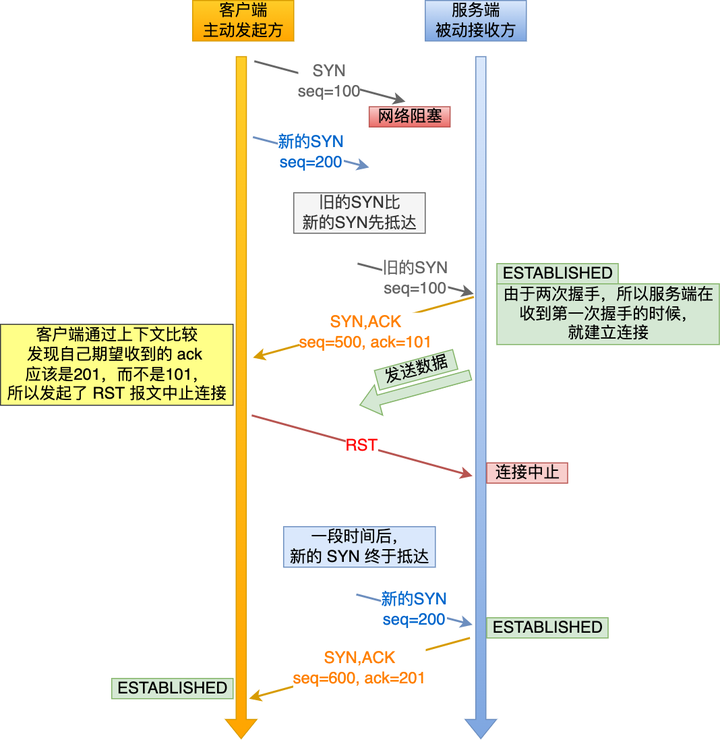
可以看到，上面这种场景下，「被动发起方」在向「主动发起方」发送数据前，并没有阻止掉历史连接，导致「被动发起方」建立了一个历史连接，又白白发送了数据，妥妥地浪费了「被动发起方」的资源。

因此，要解决这种现象，最好就是在「被动发起方」发送数据前，也就是建立连接之前，要阻止掉历史连接，这样就不会造成资源浪费，而要实现这个功能，就需要三次握手。

三次握手阻止历史连接的过程如下图，注意图中的两个连接的序列号是不一样的，因此新旧 SYN 报文并不是发生了超时重传，两个都是独立的连接。

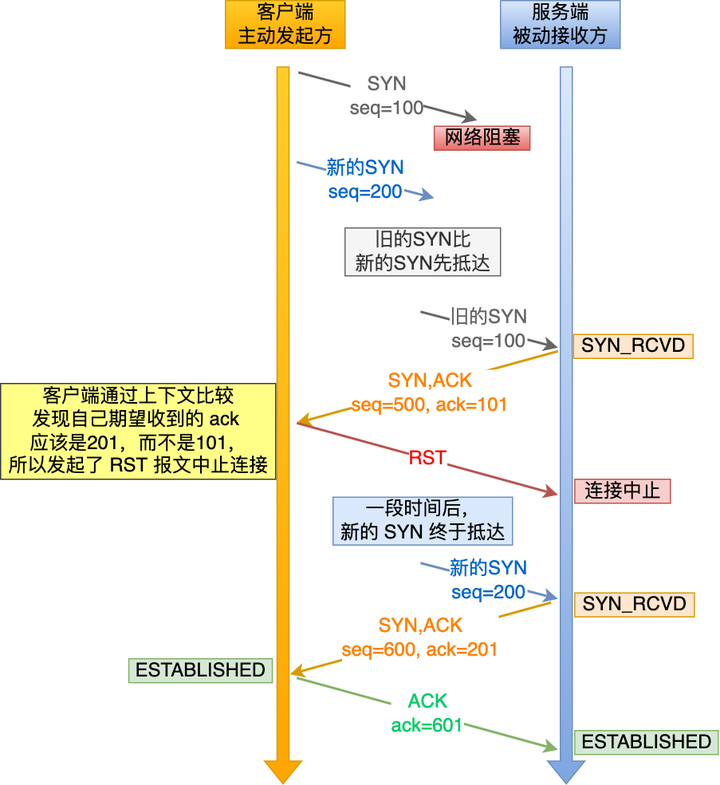
客户端连续发送多次 SYN 建立连接的报文，在网络拥堵情况下:

• 一个「旧 SYN 报文」比「最新的 SYN 」 报文早到达了服务端;
• 那么此时服务端就会回一个 SYN + ACK 报文给客户端;
• 客户端收到后可以根据自身的上下文，判断这是一个历史连接（序列号过期），那么客户端就会发送 RST 报文给服务端，表示中止这一次连接。

可以看到，在三次握手的情况下， 可以在服务端建立连接之前，可以阻止掉了历史连接，从而保证建立的连接不是历史连接。

点击关注，第一时间了解华为云新鲜技术~