[刷题] 17 Letter Combinations of a Phone Number

要求

• 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合
• 1 不对应任何字母

  

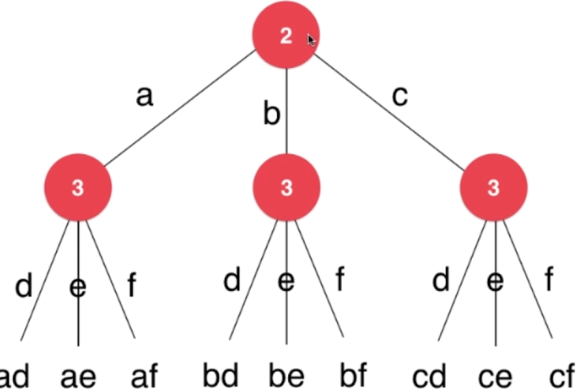
示例

• 输入：“23”
• 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]

思路

• 递归向后一位一位生成所有可能字符串
• s(digits)是digits所能生成的字符串
• letter(digits[0])是按键digits[0]对应的字符

实现

• res作为类的私有成员变量
• 调试代码：30,36,45,49

 1 #include <vector>
 2 #include <iostream>
 3 #include <string>
 4 #include <assert.h>
 5
 6 using namespace std;
 7
 8 class Solution {
 9
10 private:
11     const string letterMap[10] = {
12         " ",
13         "",
14         "abc",
15         "def",
16         "ghi",
17         "jkl",
18         "mno",
19         "pqrs",
20         "tuv",
21         "wxyz"
22     };
23
24     vector<string> res;
25     // 处理第index位数字
26     // s保存digits[0...index-1]生成的字符串
27     // 找到和digits[index]匹配的字母，获得digits[0...index]生成的解
28     void findCombination(const string &digits, int index, const string &s){
29
30         cout<<index<<" : "<<s<<endl;
31
32         // 终止条件
33         if( index == digits.size() ){
34             // s是一个解，保存
35             res.push_back(s);
36             cout<<"get "<<s<<" , return"<<endl;
37             return;
38         }
39
40         char c = digits[index];
41         assert( c >= '0' && c <= '9' && c != '1' );
42         string letters = letterMap[c-'0'];
43
44         for( int i = 0 ; i < letters.size() ; i ++ ){
45             cout<<"digits["<<index<<"] = "<<c<<" , use "<<letters[i]<<endl;
46             // 处理第index+1位数字
47             findCombination(digits, index + 1, s + letters[i] );
48         }
49         cout<<"digits["<<index<<"] = "<<c<<" complete, return"<<endl;
50         return;
51     }
52 public:
53     vector<string> letterCombinations(string digits) {
54
55         // 初始化
56         res.clear();
57         // 边界情况
58         if( digits == "" )
59             return res;
60
61         findCombination(digits, 0, "");
62
63         return res;
64     }
65 };
66
67 int main(){
68
69     vector<string> res = Solution().letterCombinations("23");
70     for( int i = 0 ; i < res.size() ; i ++ )
71         cout<<res[i]<<endl;
72
73     return 0;
74 } 

  

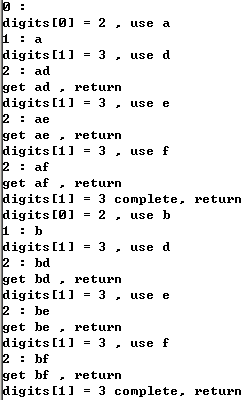
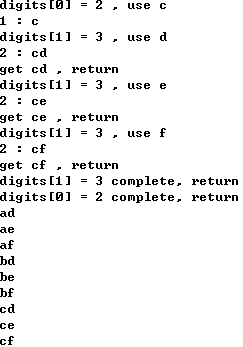
总结

• 本质是回溯（递归调用到底后，返回上一层，继续调用，直到根节点的所有可能性调用完成）
• 回溯是一种算法思想，可通过递归实现
• 和多重循环的区别在于，要处理的字符长度未知
• 动态规划的本质是在回溯的基础上进行改进，提高效率
• 复杂度：3^n（指数级O(2^n)，n个字母，每个数字3个字母）
• 暴力枚举解法，效率低，家用计算机n<20

相关

• 93 Restore IP Addresses
• 131 Palindrome Partitioning

参考

递归与回溯有什么区别？怎么区分？

https://coding.imooc.com/learn/questiondetail/19706.html