c++实现希尔密码

实验名称：

希尔密码的实现（c++版;本文只以26个大写英文字符作为加密后的密文的可选项）

实验原理：

引用知识:

记 Zm={0,1,2,...,m-1}

定义1:设A为定义在集合Zm 上的n阶方阵，若存在一个定义在Zm上的方阵B,使得

AB=BA=E(mod m)

则称A模m可逆,B为A的模m逆矩阵，记为

B=A^(-1)(modm)

定义2:设a ∈Zm若存在b∈Zm使得ab=1(mod m)，则称b为a的模m倒数或乘法逆，记作

b = a^(-1) (mod m)

命题:定义在集合Zm上的n阶方阵A模m可逆的充要条件是:m和det(A)无公共素数因子，即m 与det(A)互素。

则在模运算下解方程组:AX=Y可得如下：

X=A^(-1)^[1] (mod 26)* Y (mod 26)

下面求 A^(-1) (mod 26):

模m逆矩阵的计算：

由 |A|·A^(-1)=A* A为A的伴随矩阵

设B=KA为A的模26逆，其中k为待定系数

即：

BA=K·|A|·E

BA=E(mod26)

k·|A|=1(mod26)

k=|A|^(-1)(mod26)

故由上述所得解密矩阵的计算是由以加密矩阵行列式的值作为分母;1作为分子的分数;mod26;再乘以加密矩阵的伴随矩阵得到的矩阵;最后mod26即得到解密矩阵。

算法分析：

加密：

本次实验加密矩阵根据用户输入的阶数由系统自动随机生成，并判断是否符合模逆矩阵的条件，如果不符合就生成新的加密矩阵，直到符合条件为止；

原文加密时生成的原文矩阵阶数由加密矩阵的阶数(记作n)和原文的长度决定，由原文的长度除以加密矩阵的阶数向上取整（记作x），原文长度不够的用字符A补全。然后将原文减去字符A；

即最后会生成一个x行n列的原文矩阵；

加密过程就是用原文矩阵乘以密文矩阵得到的结果mod26。然后用结果加上字符A得到密文。

int** makeMatrix(int param,int param1) {
int** mat = new int* [param];
for (int i = 0; i < param; i++)
{
	mat[i] = new int[param1];
}
for (int i = 0; i < param; i++)
{
	for (int j = 0; j < param1; j++)
	{
		mat[i][j] = 0;
	}
}
return mat;
}
//矩阵与矩阵相乘
std::string  multiply(int **param,int**param1,int param2,int param3){
std::string sum = "";
int** mat3 = makeMatrix(param2, param3);
for (int i = 0; i < param2; i++)
{
	for (int j = 0; j <param3; j++)
	{
		for (int k = 0; k < param3; k++)
		{

			mat3[i][j] += param[i][k] * param1[k][j];

		}

		mat3[i][j] = mat3[i][j] % 26;
		sum += (int)mat3[i][j] + 'A';

	}
}
return sum;
}
//数字与矩阵相乘
int** multiply(int param,int**param1) {

//std::string sum="";
int col = _msize(param1[1]) / sizeof(int);
int** mat = makeMatrix(col, col);
for (int i = 0; i <col; i++)
{
	for (int j = 0; j < col; j++)
	{
		mat[i][j] = ((param1[i][j]* param)%26+26)%26;

	}

}

return mat;

}
//判断生成的矩阵是否合理
void judge(bool &param,int **param1,int param2) {
int det = caculate(param1,param2);
if (det%2==0||det%13==0||det<0)
{
	param = true;
}
else {
	param = false;

}

}

//加密函数入口
void  getCode() {
  std::string orignal;
  int num,zhong;
  bool flag = true;
  std::cout << "请输入原文："<<std::endl;
std::cin >> orignal;
std::cout << "请选择生成的密钥矩阵的阶数" << std::endl;
std::cin >> num;
int len = orignal.length() % num == 0 ? orignal.length() / num : orignal.length() / num + 1;
int** mat1 = makeMatrix(num,num);//密码矩阵
int** mat2 = makeMatrix(len,num);//明文矩阵
//循环创建符合密码矩阵要求的秘钥
while (flag) {
	Sleep(500);
	srand(time(NULL));
	for (int i = 0; i < num; i++)
	{
		for (int j = 0; j < num; j++)
		{
			zhong = rand() % 20;
			mat1[i][j] = zhong == 0 ? 1 : zhong;
		}

	}
	judge(flag, mat1,num);

}
//补充不能够形成矩阵的字符
int k = 0, le = num - orignal.length() % num;
for (int m = 0; m < le; m++)
{
	orignal += "A";
}
//将字符转化为原文矩阵
for (int i = 0; i <len ; i++)
{
	for (int j = 0; j < num; j++)
	{
		mat2[i][j] = (orignal[k]-'A');
		k++;
	}
}
    //矩阵相乘
std::string mtext=multiply(mat2, mat1, len, num);
std::cout << "加密矩阵" << std::endl;
for (int i = 0; i < num; i++)
{
	for (int j = 0; j < num; j++)
	{
		std::cout << mat1[i][j]<<" ";
	}
	std::cout << "" << std::endl;
}
std::cout << "密文：" << mtext << std::endl;

}

解密：

由上述的引用知识点知：解密矩阵由加密矩阵的行列式分之一mod26然后乘以加密矩阵的伴随矩阵得到的结果mod26得到。

①分数求模

对于分数求模，我借用了mod运算的分配律

(a×b) mod c=(a mod c * b mod c) mod c

即把分数求模转化为了整数求模，借助于少于30次的的循环，即可得出结果，代码如下。

注释：param参数为行列式的值mod26得到的值

int gradeMode(int param) {

for (int i = 1; ; )
{
	if ((26 * i+1) % param == 0)
	{
		return (26*i+1)/param;
		break;
	}
	i += 1;
}

}

②伴随矩阵的求解

本次实验我是用了求行列式calaulate()函数和求代数余子式surplus()函数的函数递归得到，两函数代码如下：。

int caculate(int **param,int param1){
int row = param1;
if (row==2)
{
	return param[0][0]*param[1][1]-param[0][1]*param[1][0];
}
else {
	int sum = 0;
	for (int i = 0; i < row; i++)
	{
		sum += param[0][i]*surplus(param,0,i,param1);
	}
	return sum;
}
}

int surplus(int **param,int x,int y,int param1) {
if (param1==2)
{
	return pow(-1, x + y + 2)*param[1-x][1-y];
}
else {

	int row = param1, col = param1;
	int xflag = 0, yflag = 0;
	int** mat = makeMatrix(row - 1, col - 1);
	for (int i = 0; i < row; i++)
	{
		if (i!=x)
		{
			yflag = 0;
			for (int j = 0; j < col; j++)
			{
				if (j != y )
				{
					mat[xflag][yflag] = param[i][j];
					yflag++;
				}

			}
		xflag++;
		}			

	}
	return pow(-1, x + y + 2) * caculate(mat, param1 - 1);

}

}

借助①②即可得到解密的矩阵：具体代码如下：

void putcode() {
int num;
std::string dense;
std::cout << "请输入密文" << std::endl;
std::cin >> dense;
std::cout << "请输入阶数：" << std::endl;
std::cin >> num;
int** mat1 = makeMatrix(num,num);//接受加密矩阵
int** mat2 = makeMatrix(dense.length() / num, num);//密文矩阵
int** mat3 = makeMatrix(num,num);//

std::cout << "请输入加密矩阵：" << std::endl;
    //获取加密矩阵
for (size_t i = 0; i < num; i++)
{
	for (size_t j = 0; j < num; j++)
	{
		std::cin >> mat1[i][j];
	}
}

    //转换密文维密文矩阵
int k=0;
for (size_t i = 0; i < dense.length()/num; i++)
{
	for (size_t j = 0; j < num; j++)
	{
		mat2[i][j] = (dense[k] - 'A');
		k++;
	}
}

    //算密码矩阵的伴随矩阵
for (int k = 0; k < num; k++)
{
	for (int j = 0; j < num; j++)
	{
		mat3[k][j] = surplus(mat1, j, k, num);
	}
}

int num1=caculate(mat1,num)%26;//计算行列式
int** mat4 = multiply(gradeMode(num1), mat3);//解码矩阵

for (int k = 0; k < num; k++)
{
	for (int j = 0; j < num; j++)
	{
		std::cout<<mat4[k][j]<<" " ;
	}
	std::cout << "" << std::endl;
}

std::string  original = multiply(mat2, mat4,dense.length()/num,num); //原文

std::cout << "解密结果为："<<original;

}

程序实现界面：

主程序部分代码：

#include "decode.h"
#include "Encryption.h"

void main() {
while (true)
{
	system("cls");
	int select=0;
	std::cout << "加密--1；解密--2" << std::endl;
	std::cin >> select;
	switch (select)
	{
	case 1:
		getCode();
		system("pause");
		break;
	case 2:
		putcode();
		system("pause");
		break;
	default:
		break;
	}

}

}

加密：

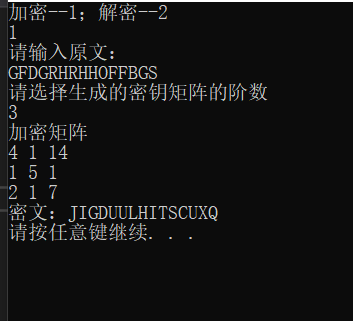
解密：

---

1. 这表示A的逆 ︎