Linux应用程序设计：用一种讨巧方式，来获取线程栈的使用信息

面对的问题

对于线程的栈空间，相信各位小伙伴都不陌生。它有下面的这几项特性：

> 1. 由操作系统分配固定的空间;

>

> 2. 使用一个栈寄存器来保存实时位置;

>

> 3. 后进先出。

今天，我们不聊操作系统层面对栈的管理，只从应用程序的角度，来看一下如何实时获取栈的使用情况。

在一般的单片机/嵌入式程序开发过程中，在创建一个线程(或者称作任务)的时候，是可以指定给该线程分配多少栈空间的。

然后在调试的时候呢，周期性的打印出栈区的使用情况：消耗了多少空间，还剩余多少空间。

这样的话，跑完每一个测试用例之后，就能得到一个大致的统计数据，从而最终决定：需要给这个线程分配多少栈空间。

例如：在 ucOS 系统中，提供了函数 NT8U OSTaskStkChk(INT8U prio, OS_STK_DATA *p_stk_data)，来获取一个任务的栈使用信息。

但是在 Linux 系统中，并没有这样类似的函数，来直接获取栈使用信息。

因此，为了得到此线程的已使用和空闲栈空间，必须通过其他的方式来获取。

下面，就提供 2 种解决方案：正规军方式和杂牌军方式！

正规军方式

在 Linux 系统中，在创建一个线程的时候，是可以通过线程属性来设置：为这个线程分配多少的栈(stack)空间的。

如果应用程序不指定的话，操作系统就设置为一个默认的值。

线程创建完毕之后，操作系统在内核空间，记录了这个线程的一切信息，当然也就包括给它分配的栈空间信息。

为了让应用层能够获取到这个信息，操作系统也提供了相应的系统函数。代码如下：

pthread_attr_t attr;
void *stack_addr;
int stack_size;

memset(&attr, 0, sizeof(pthread_attr_t));
pthread_getattr_np(pthread_self(), &attr);
pthread_attr_getstack(&attr, &stack_addr, &stack_size);
pthread_attr_destroy(&attr);

printf("statck top   = %p \n", stack_addr);
printf("stack bottom = %p \n", stack_addr + stack_size);

从上面这段代码中可以看到，它只能获取栈空间的地址开始以及总的空间大小，仍然不知道当前栈空间的实际使用情况！

我找了一下相关的系统调用，Linux 似乎没有提供相关的函数。

怎么办？只能迂回操作。

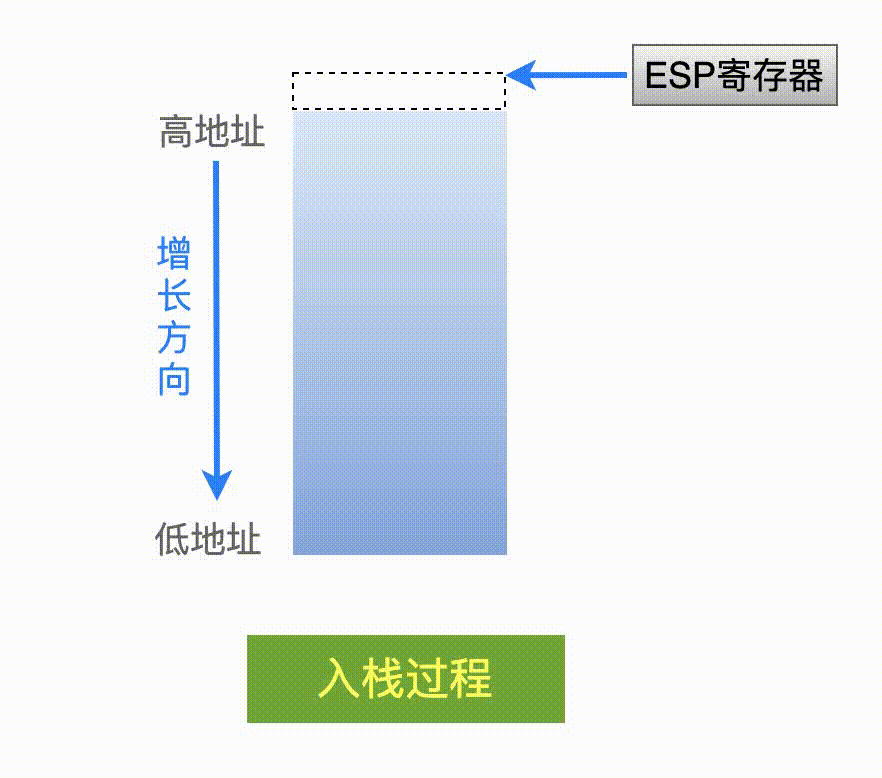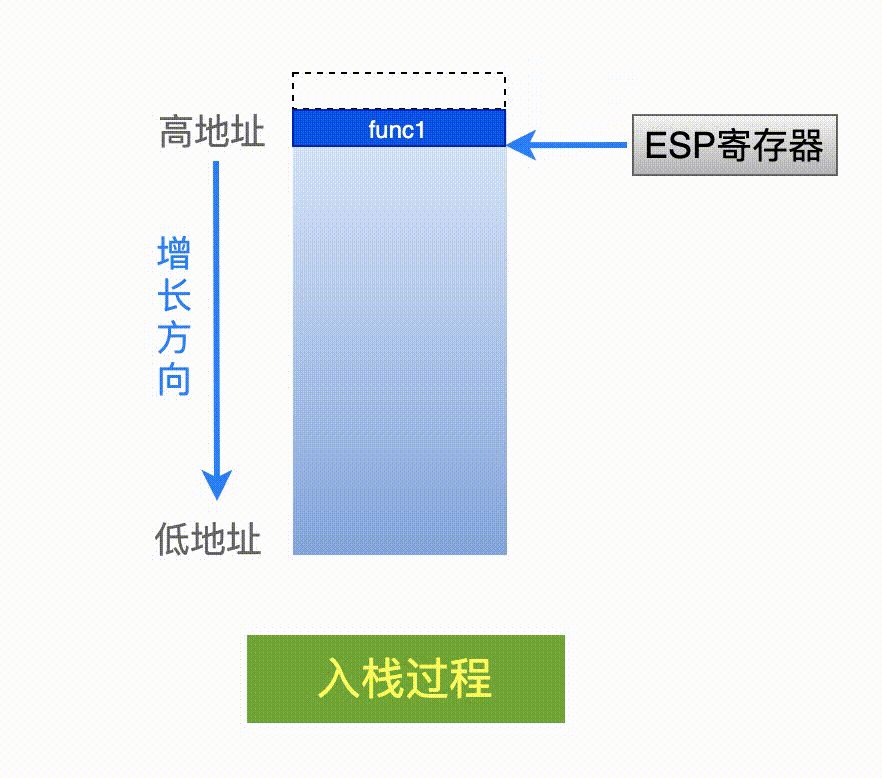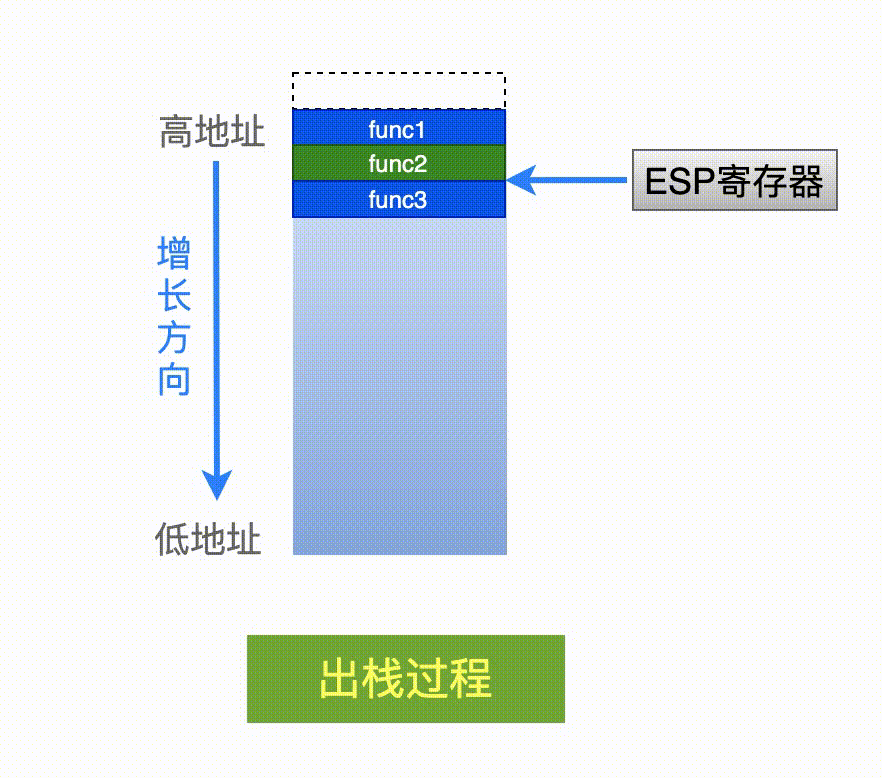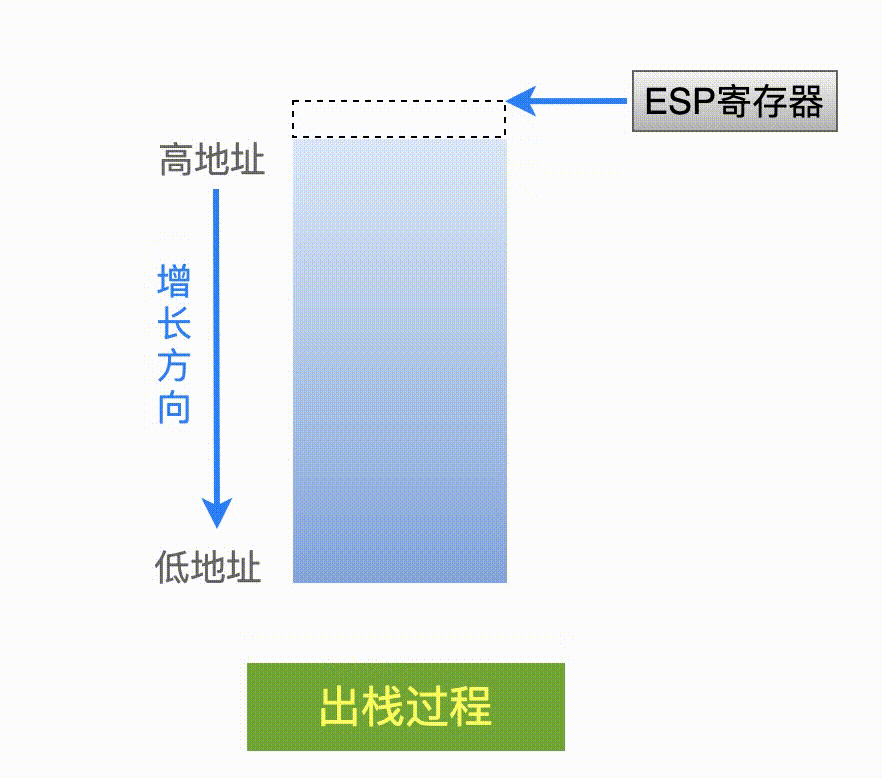
我们知道，在 Linux x86 平台上，寄存器 ESP 就是来存储栈指针的。对于一个满递减类型的栈，这个寄存器里的值，就代表了当前栈中最后背使用的、那个栈空间的地址。

因此，只要我们能够获取到 ESP 寄存器里的值，就相当于知道了当前这个栈有多少空间被使用了。

那么怎样来获取 ESP 寄存器的值呢？ 既然是寄存器，那就肯定是使用汇编代码了。

很简单，就 1 行：

size_t esp_val;
asm("movl %%esp, %0" : "=m"(esp_val) :);

对不起，我错了！应该是 2 行代码，忘记变量定义了。

对于汇编代码不熟悉的小伙伴，可以参考之前总结的一篇文章：内联汇编很可怕吗？看完这篇文章，终结它！

找到第 4 个示例，直接抄过来就行。

好了，拿到了以上的所有信息，就可以计算出栈的已使用和空闲空间的大小了：

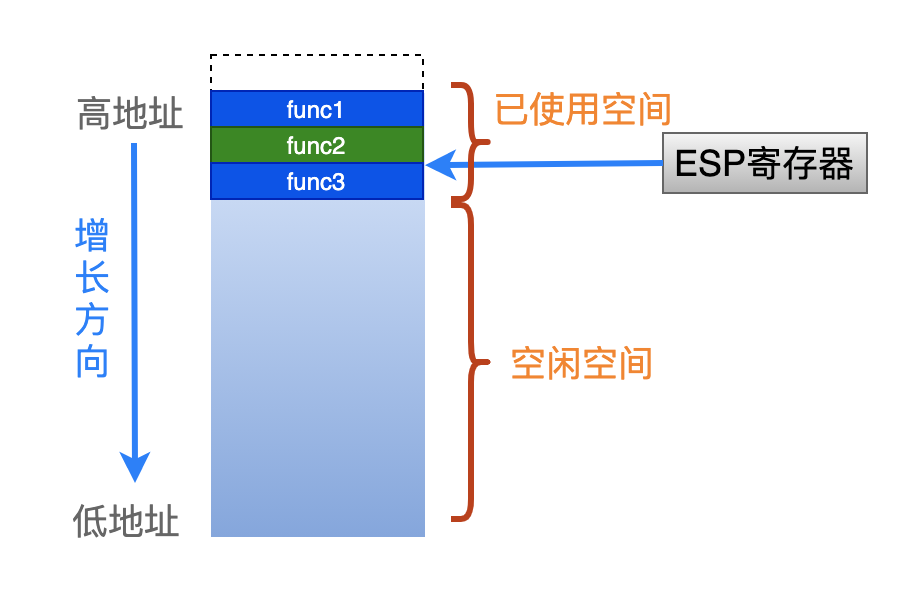
把以上代码放在一起：

#include <unistd.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <pthread.h>
#include <sys resource.h="">

void print_stack1()
{
    size_t used, avail;
    pthread_attr_t attr;
    void *stack_addr;
    int stack_size;

    // 获取栈寄存器 ESP 的当前值
    size_t esp_val;
    asm("movl %%esp, %0" : "=m"(esp_val) :);

    // 通过线程属性，获取栈区的起始地址和空间总大小
    memset(&amp;attr, 0, sizeof(pthread_attr_t));
    pthread_getattr_np(pthread_self(), &amp;attr);
    pthread_attr_getstack(&amp;attr, &amp;stack_addr, &amp;stack_size);
    pthread_attr_destroy(&amp;attr);

    printf("espVal = %p \n", esp_val);
    printf("statck top   = %p \n", stack_addr);
    printf("stack bottom = %p \n", stack_addr + stack_size);

    avail = esp_val - (size_t)stack_addr;
    used = stack_size - avail;

    printf("print_stack1: used = %d, avail = %d, total = %d \n",
            used, avail, stack_size);
}

int main(int argc, char *agv[])
{
    print_stack1();
    return 0;
}

杂牌军方式

上面的正规军方法，主要是通过系统函数获取了线程的属性信息，从而获取了栈区的开始地址和栈的总空间大小。

为了获取这两个值，调用了 3 个函数，有点笨重！

不知各位小伙伴是否想起：Linux 操作系统会为一个应用程序，都提供了一些关于 limit 的信息，这其中就包括堆栈的相关信息。

这样的话，我们就能拿到一个线程的栈空间总大小了。

此时，还剩下最后一个变量不知道：栈区的开始地址！

我们来分析一下哈：当一个线程刚刚开始执行的时候，栈区里可以认为是空的，也就是说此时 ESP 寄存器里的值就可以认为是指向栈区的开始地址！

是不是有豁然开朗的感觉？！

但是，这仍然需要调用汇编代码来获取。

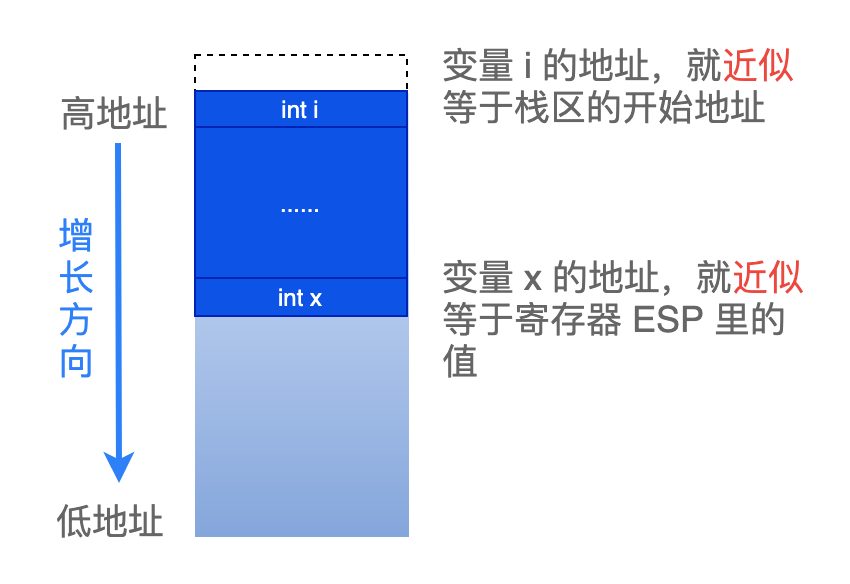
再想一步，既然此时栈区里可以认为是空的，那么如果在线程的第一个函数中，定义一个局部变量，然后通过获取这个局部变量的地址，不就相当于是获取到了栈区的开始地址了吗?

如下图所示：

我们可以把这个局部变量的地址，记录在一个全局变量中。然后在应用程序的其他代码处，就可以用它来代表栈的起始地址。

知道了 3 个必需的变量，就可以计算栈空间的使用情况了：

// 用来存储栈区的起始地址
size_t top_stack;

void print_stack2()
{
    size_t used, avail;

    size_t esp_val;
    asm("movl %%esp, %0" : "=m"(esp_val) :);
    printf("esp_val = %p \n", esp_val);

    used = top_stack - esp_val;

    struct rlimit limit;
    getrlimit(RLIMIT_STACK, &limit);
    avail = limit.rlim_cur - used;
    printf("print_stack2: used = %d, avail = %d, total = %d \n",
            used, avail, used + avail);
}

int main(int argc, char *agv[])
{
    int x = 0;
    // 记录栈区的起始地址(近似值)
    top_stack = (size_t)&x;
    print_stack2();
    return 0;
}

更讨巧的方式

在上面的两种方法中，获取栈的当前指针位置的方式，都是通过汇编代码，来获取寄存器 ESP 中的值。

是否可以继续利用刚才的技巧：通过定义一个局部变量的方式，来间接地获取 ESP 寄存器的值？

void print_stack3()
{
    int x = 0;
    size_t used, avail;
    // 局部变量的地址，可以近似认为是 ESP 寄存器的值
    size_t tmp = (size_t)&x;
    used =  top_stack - tmp;

    struct rlimit limit;
    getrlimit(RLIMIT_STACK, &limit);
    avail = limit.rlim_cur - used;
    printf("print_stack3: used = %d, avail = %d, total = %d \n",
            used, avail, used + avail);
}

int main(int argc, char *agv[])
{
    int x = 0;
    top_stack = (size_t)&x;
    print_stack3();
    return 0;
}

总结

以上的几种方式，各有优缺点。

我们把以上 3 个打印堆栈使用情况的函数放在一起，然后在 main 函数中，按顺序调用 3 个测试函数，每个函数中都定义一个整型数组(消耗 4K 的栈空间)，然后看一下这几种方式的打印输出信息：

// 测试代码(3个打印函数就不贴出来了)
void print_stack1()
{
    ...
}

void print_stack2()
{
    ...
}

void print_stack3()
{
    ...
}

void func3()
{
    int num[1024];
    print_stack1();
    printf("\n\n ********* \n");
    print_stack2();
    printf("\n\n ********* \n");
    print_stack3();
}

void func2()
{
    int num[1024];
    func3();
}

void func1()
{
    int num[1024];
    func2();
}

int main(int argc, char *agv[])
{
    int x = 0;
    top_stack = (size_t)&x;
    func1();
    return 0;
}

打印输出信息：

espVal = 0xffe8c980
statck top   = 0xff693000
stack bottom = 0xffe90000
print_stack1: used = 13952, avail = 8362368, total = 8376320 

 *********
esp_val = 0xffe8c9a0
print_stack2: used = 12456, avail = 8376152, total = 8388608 

 *********
print_stack3: used = 12452, avail = 8376156, total = 8388608

------ End ------

让知识流动起来，越分享越幸运！

Hi~，我是道哥，嵌入式开发老兵。



星标公众号，能更快找到我！

推荐阅读

【1】C语言指针-从底层原理到花式技巧，用图文和代码帮你讲解透彻

【2】一步步分析-如何用C实现面向对象编程

【3】原来gdb的底层调试原理这么简单

【4】内联汇编很可怕吗？看完这篇文章，终结它！

【5】都说软件架构要分层、分模块，具体应该怎么做

</pthread.h></string.h></stdlib.h></stdio.h></unistd.h>