Covered Points Count CF1000C 思维 前缀和 贪心

 Covered Points Count

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn segments on a coordinate line; each endpoint of every segment has integer coordinates. Some segments can degenerate to points. Segments can intersect with each other, be nested in each other or even coincide.

Your task is the following: for every k∈[1..n]k∈[1..n], calculate the number of points with integer coordinates such that the number of segments that cover these points equals kk. A segment with endpoints lili and riri covers point xx if and only if li≤x≤rili≤x≤ri.

Input

The first line of the input contains one integer nn (1≤n≤2⋅1051≤n≤2⋅105) — the number of segments.

The next nn lines contain segments. The ii-th line contains a pair of integers li,rili,ri (0≤li≤ri≤10180≤li≤ri≤1018) — the endpoints of the ii-th segment.

Output

Print nn space separated integers cnt1,cnt2,…,cntncnt1,cnt2,…,cntn, where cnticnti is equal to the number of points such that the number of segments that cover these points equals to ii.

Examples

input

Copy

3
0 3
1 3
3 8

output

Copy

6 2 1 

input

Copy

3
1 3
2 4
5 7

output

Copy

5 2 0 

Note

The picture describing the first example:

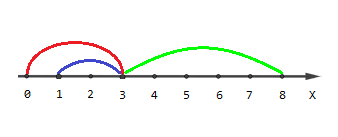
Points with coordinates [0,4,5,6,7,8][0,4,5,6,7,8] are covered by one segment, points [1,2][1,2] are covered by two segments and point [3][3] is covered by three segments.

The picture describing the second example:

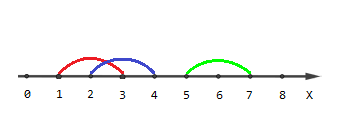
Points [1,4,5,6,7][1,4,5,6,7] are covered by one segment, points [2,3][2,3] are covered by two segments and there are no points covered by three segments.

给你n条线段的开始点和结束点，问被1-n条线段覆盖的点的个数

记录每个点的位置，以及他是开始点还是结束点，放在一个数组里。然后按从小到大排序，用一个cnt记录下现在覆盖了几条线段，接着直接遍历，加上每段点数，遇到开始点cnt+1，遇到结束点cnt-1

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl
using namespace std;
const int maxn = 5e5 + ;
const int mod = 1e9 + ;
typedef long long ll;
struct node {
    ll first, second;
};
node a[maxn];
ll ans[maxn];
bool cmp( node p, node q ) {
    return p.first < q.first;
}
int main() {
    ll n;
    while( cin >> n ) {
        memset( ans, , sizeof(ans) );
        for( ll i = ; i <= n; i ++ ) {
            ll l, r;
            cin >> l >> r;
            a[i*-].first = l, a[i*].first = r+;
            a[i*-].second = , a[i*].second = -;
        }
        ll cnt = ;
        sort( a + , a + *n + , cmp );
        for( ll i = ; i <= *n; i ++ ) {
            ans[cnt] += a[i].first - a[i-].first;
            cnt += a[i].second;
        }
        for( ll i = ; i <= n; i ++ ) {
            if( i != n ) {
                cout << ans[i] << " ";
            } else {
                cout << ans[i] << endl;
            }
        }
    }
    return ;
}