使用excel计算骰子输赢概率

如何得到使用3个骰子掷赢4个骰子的概率（每个骰子的点数为1-6，点数一样算输）

分为3步解决：

第一步.计算n个骰子得到m点数的分布

1个骰子能得到1、2、3、4、5、6点数，每个点数出现的方式只有1种。

2个骰子能得到2、3。。。12点数，每个点数出现的方式有1、2、3。。。1种。

推导：F(n,m)为n个骰子得到m点数的排列方式

第n个骰子得到1...6点数的方式分别为1种

易得到 F(n, m) = f(n-1, m-1) + f(n-1, m-2) + f(n-1, m-3) + f(n-1, m-4) + f(n-1, m-5)

使用Exce很容易得到结果，如下图所示。只需填好第一列数值，后面几列用excel的sum函数轻松得到。

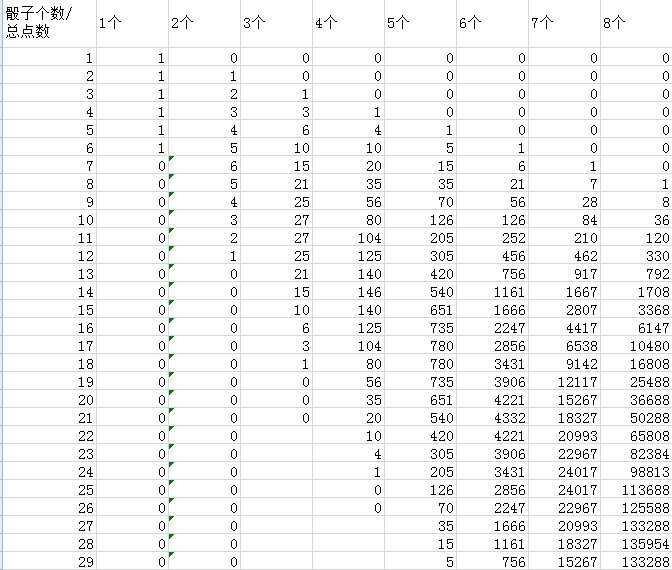
归一化得到概率 R(n, m)

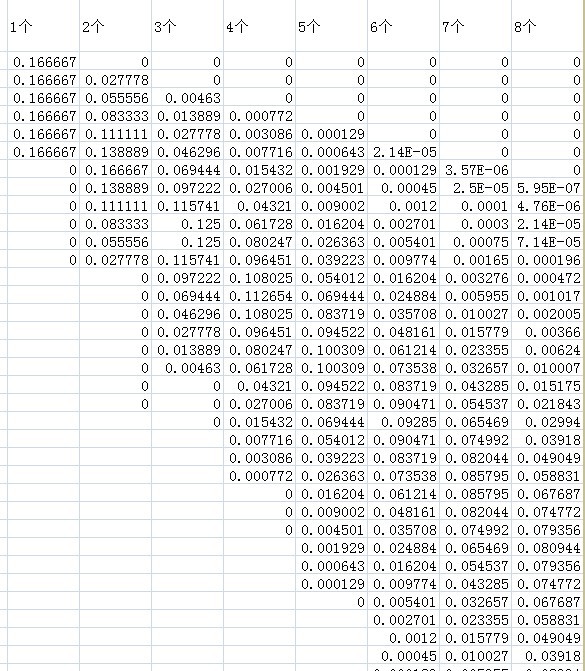
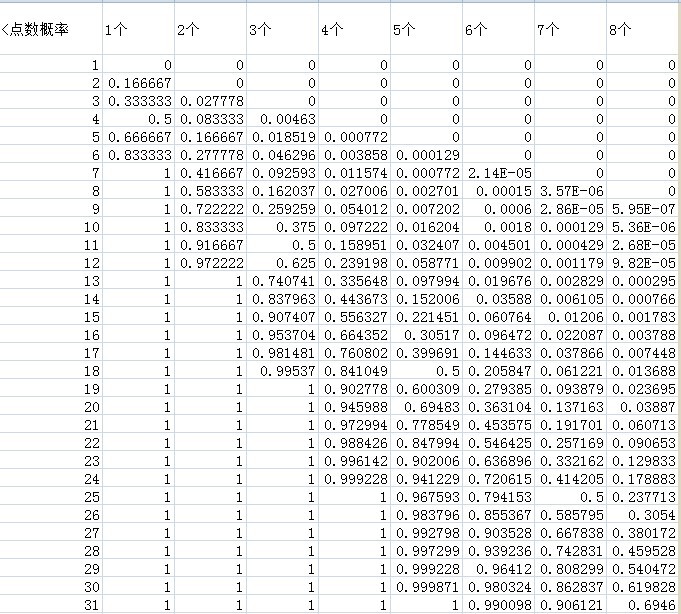
第二步.计算n个骰子掷得点数小于m的概率

H(n, m) = R(n,1) + ... + R(n, m-1)

同理，使用excel将上表的数据，得到

第三步.计算x个骰子掷赢y个骰子的概率

G(x,y) = ΣR(x,k) * H(y,k)    (k从1到x*6)

继续excel，得到如下

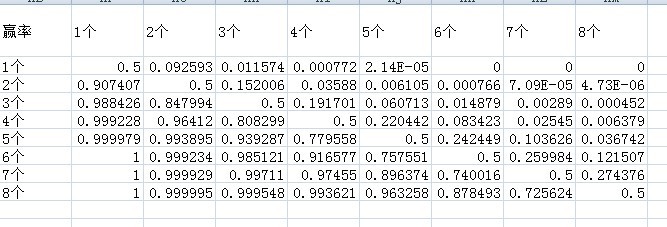
如上图所示，3个骰子掷赢4个骰子的概率是0.191701，好像不是很高。

小结：感觉excel还是很强大的，很多复杂的算法经过简单的拆分和公式推导，很容易实现。而且预先得到结果，比代码实时计算更靠谱，更效率。