简单的量子算法(二)：Simon's Algorithm

前情回顾：

简单的量子算法(一)：Hadamard 变换、Parity Problem

好的，现在开始正版的故事，Simon’s Algorithm

问题：

有一个secret string，是n位的0，1串 $s \in \{0,1 \} ^n$

现在有一个黑盒子，f(x)，我们对他唯一的了解就是 $f(x)=f(x \oplus s)$ ，输入的x也是n位的0，1串 $x \in \{0,1 \} ^n$

请问，要多少次，我们可以找到这个secret string?

经典解法：

如果我们能找到 $x$ 和 $x \oplus s$ ，那么非常容易，就可以得到s，只要 $x\oplus x\oplus s$ 。

那么如果找到两个输入拥有相同的输出呢？

这个问题其实是另一个大家都很熟悉的问题的变形，一群人中，要多少人就有两个人的生日是相同的，印象中，23人两个人的生日是相同的概率就大于50%了，如果有60个人，那么两个人生日相同的概率就超过99%了。

这个问题和生日问题的解法是一样的，就不再累述了，想要知道的请搜索生日问题，在这里，我们给出一个大概的答案，是 $2^{n/2}$ c次。

量子解法：

量子解法一共有三步：

set up random superposition $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$
Fourier Sample to get a random y: $y·s=0 (\mod 2)$
repeat step n-1 times to generate n-1 linear equation.

接下来，我们来一步一步的看每个步骤在做什么，以及怎么做：

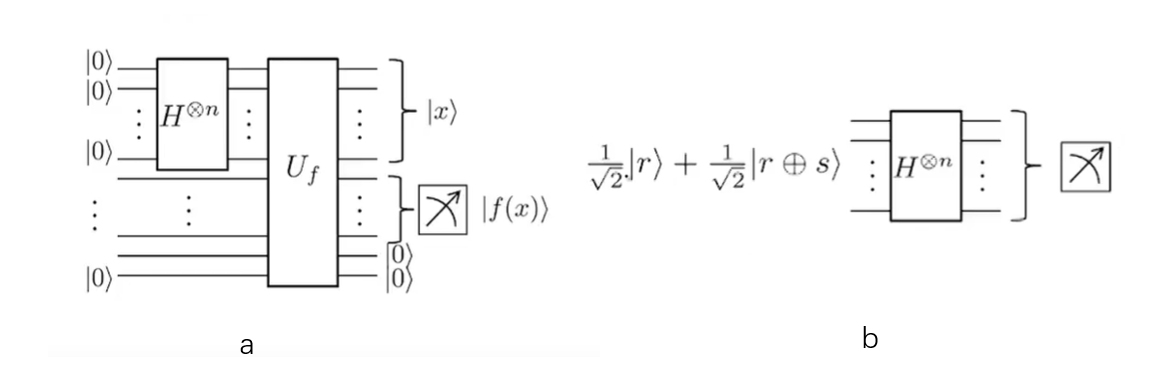
第一步，制造叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$ ，这个可以通过图a实现。

首先通过第一个$H ^{\otimes n}$ 门，我们n比特的 $|0\rangle$ 就成功的变成了叠加态 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle $

和 $|b\rangle$ 一起通过 $U_f$ ，得到的结果是 $\frac{1}{2^{\frac{n}{2}}} \sum_x |x\rangle|b\oplus f(x) \rangle $

至此我们得到了想要的叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$

第二步，Fourier Sampling

对我们得到的叠加态 $ \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle$ Fourier Sampling

再次通过$H ^{\otimes n}$ 我们能得到什么？

依照我们在简单的量子算法(一)中的结论，我们知道 $H^{\otimes n} |u\rangle = \sum_x \frac{-1^{u·x}}{2^{\frac{n}{2}}} |x\rangle$ 。

那么

\[\begin{align} H^{\otimes n} ( \frac{1}{\sqrt2} |r\rangle +\frac{1}{\sqrt2} |r \oplus s \rangle) &= \frac{1}{\sqrt2}\sum_x \frac{-1^{r·x}}{2^{n/2}} |x\rangle+\frac{1}{\sqrt2}\sum_x \frac{-1^{(r\oplus s)·x}}{2^{n/2}} |x\rangle \\ &=\sum_x (\frac{-1^{r·x}}{2^{(n+1)/2}}+\frac{-1^{(r\oplus s)·x}}{2^{(n+1)/2}}) |x\rangle \\ &= \sum_x\frac{1^{r·x}+(-1)^{(r\oplus s)·x}}{2^{(n+1)/2}}|x\rangle \end{align}\]

此时，我们的问题已经集中在了 $1^{r·x}+(-1)^{(r\oplus s)·x}$ 上。

$(-1)^{(r\oplus s)·x}$ 可以写成$(-1)^{s·x}*(-1)^{r·x}$ （至于为什么可以，大家可以试一下都是按位操作，一共也就4种可能

那么每种可能的概率的公式就可以写成$\frac{（(-1)^{s·x}+1）*(-1)^{r·x}}{2^{(n+1/2)}}$

如果 $s·x=0$ 那么，这个概率正好为 $\frac{(-1)^{r·z}}{2^{(n-1)/2}}$

如果 $s·x=-1$ 那么，这个概率正好为0

那么这又说明了什么呢？

这个说明只要我们测量 $|x\rangle$ ，那么我们得到的x一定是 $s·x=0$ 的，因为不为0的都被抵消了。

那么得到了x，又意味着什么呢？

$s·x=0$ 事实上我们是得到了一个等式 $s_1x_1+s_2x_2+……+s_nx_n =0 \mod 2 $

第三步：

如果我们把第一次测量得到的x编号为 $x^1$ ，那么我们得到了等式 $s_1x_1^1+s_2x_2^1+……+s_nx_n^1 =0 \mod 2 $

第二次测量，得到等式 $s_1x_1^1+s_2x_2^1+……+s_nx_n^1 =0 \mod 2 $

以此类推，测量n-1次，得到了n-1个等式的方程式组。

$s_1x_1^1+s_2x_2^1+……+s_nx_n^1 =0 \mod 2 $

……

$s_1x_1^{n-1}+s_2x_2^{n-1}+……+s_nx_n^{n-1} =0 \mod 2 $

n-1个等式，n个未知数( $s_1,s_2,……,s_n$ )，一般来说会有两组解，一组是全零的平凡解，这个是我们不要的，而另一组解就是我们的答案 $s$ 。

成功的概率：

上述的解方程有一个前提，那就是这是一个线性方程组，如果这个不是线性的，那么测量n-1次是不可能得答案的。

那么我测量得到的x组成的方程是线性方程的概率是多少呢？

我们可以列一个表格来看看：

	失败的情况	失败的概率	成功的概率
$x^1$	0	$\frac{1}{2^{n-1}}$	$1-\frac{1}{2^{n-1}}$
$x^2$	0、 $x^1$	$\frac{2}{2^{n-1}}$	$1-\frac{1}{2^{n-2}}$
$x^3$	0 、 $x^1$ 、$x^2$ 、$x^1+x^2$	$\frac{4}{2^{n-1}}$	$1-\frac{1}{2^{n-3}}$
……	……	…………	$1-\frac{1}{2^{n-1}}$
$x^{n-1}$	0 、 $x^1$ ……$x^1+x^2$……$x^1+x^2+……+x^n-2$	$\frac{2^{n-2}}{2^{n-1}}$	$1-\frac{1}{2}$

每次的测量失败的情况分为以下三种情况：

测量出来全是0
测量出来结果和前面的是一样的
测量出来的结果是前面测量结果的线性组合

因为这里算的成功概率都是独立的成功概率，所以要算整体的成功概率是他们的乘积

$\frac{1}{2}*\frac{3}{4}*\frac{7}{8}*……*\frac{2^{n-1}-1}{2^{n-1}}$

上面这个式子求极限是一个q series的问题，感兴趣的朋友可以去查一下怎么求解，这里直接给出概率，约等于0.28878

注意：

大家是不是以为这样子就万事大吉了？

No，这里还有一个需要注意的地方，可能很多朋友已经意识到了，量子态不是测量完就坍塌吗？为什么可以测量n-1次？

事实上，这是把第一部分给做了n-1次，这样你才可以有n-1个 $|x\rangle$ 给你测量找出满足线性条件的x。

参考资料：

Quantume Mechanics & Quantume Computation Lecture 8