原码、反码、补码和移码事实上非常easy

近期在备战软考，复习到计算机组成原理的时候，看到书中关于原码、反码、补码和移码的定义例如以下(n是机器字长)：

原码：

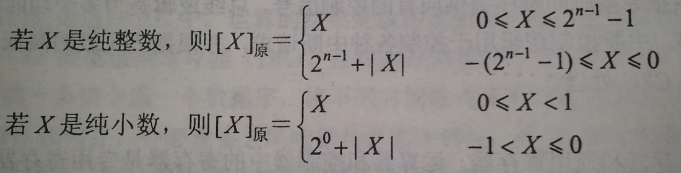
反码：

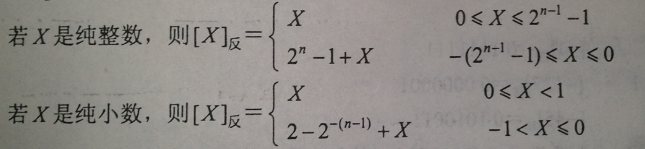
补码：

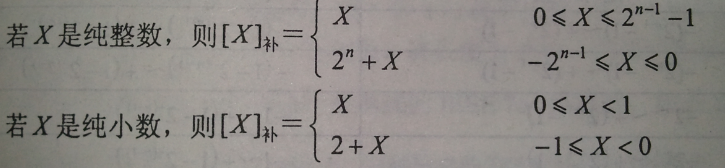
移码：

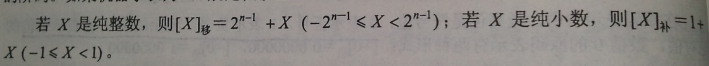
看完这些定义以后，我的脑袋瞬间膨胀到原来的二倍！这样变态的公式无论你记不记得住，反正我是记不住！还好曾经对它们有所了解，否则看到这一堆公式恐怕我早就放弃參加软考的念头喽。

事实上不是必需弄得这么麻烦，它们全然能够用一两句话就描写叙述的非常清楚。

原码：

假设机器字长为n，那么一个数的原码就是用一个n位的二进制数，当中最高位为符号位：正数为0，负数为1。剩下的n-1位表示概数的绝对值。

比如： X=+101011 , [X]原= 00101011    X=-101011
, [X]原= 10101011 

位数不够的用0补全。

PS：正数的原、反、补码都一样：0的原码跟反码都有两个，由于这里0被分为+0和-0。

反码：

知道了什么是原码，那反码就更是张飞吃豆芽——小菜一碟了。知道了原码，那么你仅仅须要具备区分0跟1的能力就能够轻松求出反码，为什么呢？由于反码就是在原码的基础上，符号位不变其它位按位取反(就是0变1，1变0)就能够了。

比如：X=-101011 , [X]原= 10101011
，[X]反=11010100

补码：

补码也很的简单就是在反码的基础上依照正常的加法运算加1。

比如：X=-101011
, [X]原= 10101011 ，[X]反=11010100，[X]补=11010101

PS：0的补码是唯一的，假设机器字长为8那么[0]补=00000000。

移码：

移码最简单了，无论正负数，仅仅要将其补码的符号位取反就可以。

比如：X=-101011
, [X]原= 10101011 ，[X]反=11010100，[X]补=11010101，[X]移=01010101

PS：很感谢12楼对负数补码的补充

以上内容仅仅适合刚開始学习的人參考，高手勿喷，有说的不正确的地方欢迎指出，感激不尽！