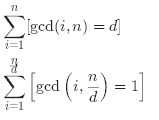[SDOi2012]Longge的问题(洛谷 2303)
题目描述
Longge的数学成绩非常好,并且他非常乐于挑战高难度的数学问题。现在问题来了:给定一个整数N,你需要求出∑gcd(i, N)(1<=i <=N)。
输入格式
一个整数,为N。
输出格式
一个整数,为所求的答案。
输入输出样例
6
15
说明/提示
对于60%的数据,0<N<=2^16
对于100%的数据,0<N<=2^32
本题的重点便在于该如何转化原式∑gcd(i, N),下面我给出变化过程:(时间复杂度: 因子个数*√n)
注意,上面的↓↓↓这一步可以说是肥肠常用了!
那么这道题自然就变成了求欧拉函数值的模板题,但同时还有一点优化小技巧,在枚举最大公约数d的时候(代码里写的是i),可以顺便把n/d也一起算。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n;
ll phi(ll n)
{
ll ans=n;
for(register ll i=;i*i<=n;i++)
if(n%i==)
{
ans=ans/i*(i-);
while(n%i==)n/=i;
}
if(n>)ans=ans/n*(n-);
return ans;
}
ll ff(ll x)
{
ll res=0LL,i=1LL;
for(;i*i<x;i++)
if(x%i==)res+=i*phi(x/i)+(x/i)*phi(i);
if(i*i==x)res+=i*phi(i);
return res;
}
int main()
{
scanf("%lld",&n);
printf("%lld",ff(n));
return ;
}
代码来咯
//参考:Siyuan 的博客
[SDOi2012]Longge的问题(洛谷 2303)的更多相关文章
- 洛谷 P2303 [SDOi2012]Longge的问题 解题报告
P2303 [SDOi2012]Longge的问题 题目背景 SDOi2012 题目描述 Longge的数学成绩非常好,并且他非常乐于挑战高难度的数学问题.现在问题来了:给定一个整数\(N\),你需要 ...
- 洛谷 P5785 [SDOI2012] 任务安排
链接: P5785 弱化版:P2365 题意: 有 \(n\) 个任务待完成,每个任务有一个完成时间 \(t_i\) 和费用系数 \(f_i\),相邻的任务可以被分成一批.从零时刻开始这些任务会被机器 ...
- 洛谷 P2120 [ZJOI2007] 仓库建设
链接: P2120 题意: 有 \(n\) 个点依次编号为 \(1\sim n\).给出这 \(n\) 个点的信息,包括位置 \(x_i\),所拥有的的物品数量 \(p_i\),在此建设一个仓库的费用 ...
- BZOJ 2705: [SDOI2012]Longge的问题 [欧拉函数]
2705: [SDOI2012]Longge的问题 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 2553 Solved: 1565[Submit][ ...
- 洛谷1640 bzoj1854游戏 匈牙利就是又短又快
bzoj炸了,靠离线版题目做了两道(过过样例什么的还是轻松的)但是交不了,正巧洛谷有个"大牛分站",就转回洛谷做题了 水题先行,一道傻逼匈牙利 其实本来的思路是搜索然后发现写出来类 ...
- 洛谷P1352 codevs1380 没有上司的舞会——S.B.S.
没有上司的舞会 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description Ural大学有N个职员,编号为1~N.他们有 ...
- 洛谷P1108 低价购买[DP | LIS方案数]
题目描述 “低价购买”这条建议是在奶牛股票市场取得成功的一半规则.要想被认为是伟大的投资者,你必须遵循以下的问题建议:“低价购买:再低价购买”.每次你购买一支股票,你必须用低于你上次购买它的价格购买它 ...
- 洛谷 P2701 [USACO5.3]巨大的牛棚Big Barn Label:二维数组前缀和 你够了 这次我用DP
题目背景 (USACO 5.3.4) 题目描述 农夫约翰想要在他的正方形农场上建造一座正方形大牛棚.他讨厌在他的农场中砍树,想找一个能够让他在空旷无树的地方修建牛棚的地方.我们假定,他的农场划分成 N ...
- 洛谷P1710 地铁涨价
P1710 地铁涨价 51通过 339提交 题目提供者洛谷OnlineJudge 标签O2优化云端评测2 难度提高+/省选- 提交 讨论 题解 最新讨论 求教:为什么只有40分 数组大小一定要开够 ...
随机推荐
- AtomicReference示例
对引用类型的原子性操作 /** * *对引用变量的原子操作 note: *在java中对引用类型的变量,赋值是原子性的,为什么还要有atomicReference,假如要对一个引用类型进行比较,设置等 ...
- jdk1.8 Stream 特性总结
不是数据结构 它没有内部存储,它只是用操作管道从 source(数据结构.数组.generator function.IO channel)抓取数据. 它也绝不修改自己所封装的底层数据结构的数据.例如 ...
- 《即时消息技术剖析与实战》学习笔记6——IM系统如何保证消息的安全性
在消息产生.流转的各个环节中,需要保证消息传输安全性.消息存储安全性.消息内容安全性. 一.消息传输安全性 消息传输的重要防范点有两个,一是访问入口安全,二是传输链路安全. 1.HttpDNS保证访问 ...
- file 从InputStream读取byte[]示例
file 从InputStream读取byte[]示例 分类专栏: java基础 public static byte[] getStreamBytes(InputStream is) throw ...
- FormData的Ajax提交注意事项
Ajax提交表单一般有下面两种形式: var form_data = $('#form').serialize(); var form_data = new FormData($('#form')[0 ...
- vue 强制刷新 demo 神器
this.$forceUpdate() /*关键句,强制更新dom*/
- tcbRouter
tcb-router 基于koa风格的小程序·云开发云函数轻量级类路由库,主要用于优化服务端函数处理逻辑 安装 在云函数当前目录下安装:npm install --save tcb-router 使 ...
- 递归删除文件和文件夹(bat)
递归删除当前目录下指定的文件和文件夹,使用了通配符,Win10下亲测有效,仅供参考! Batch Code 123456 @echo off echo del file... for /r % ...
- make CMake 来龙去脉
理论上说,任意一个C++程序都可以用g++来编译. 大家都知道,写程序大体步骤如下: 1.用编辑器编写源代码,如.c文件. 2.用编译器编译代码生成目标文件,如.o. 3.用链接器连接目标代码生成可执 ...
- contab路径问题(脚本调用另一个文件)
问题描述 当在定时任务里,要执行一个脚本A,然后A脚本需要调用另一个文件B,此时定时任务执行不成功,会报错找不到文件 解决办法 先cd到放执行脚本的路径,这样就在定时任务的脚本里可以调用相对路径下 ...