常见的概率分布类型（二）（Probability Distribution II）

以下是几种常见的离散型概率分布和连续型概率分布类型：

伯努利分布（Bernoulli Distribution）：常称为0-1分布，即它的随机变量只取值0或者1。

伯努利试验是单次随机试验，只有"成功"（1）或"失败"（0）这两种结果。假如某次伯努利实验成功的概率为p，失败的概率为q=1-p，那么实验成功或失败的概率可以写成：。

伯努利分布的期望：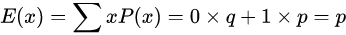

伯努利分布的方差：

二项分布（Binomial Distribution）：用以描述n次独立的伯努利实验中有x次成功的概率。

假如每次伯努利实验成功的概率为p，失败的概率为q=1-p，那么n次独立的伯努利实验中有x次成功的概率是：。这就是二项分布的概率质量函数。

二项分布的期望：E(x)=μ=np

二项分布的方差：Var(x)=σ²=npq

最常见的二项分布问题就是多次投硬币：投掷10次均匀的硬币，其中恰好有5次正面朝上的概率是多少？

投掷10次均匀的硬币，其中至少有8次正面朝上的概率是多少？

当n>50，p<0.1时，二项分布可以转换成泊松分布。

当np>5以及nq>5时，二项分布可以转换成正态分布。但是由于正态分布是连续变量，所以需要加一个continuity correction，例如：P(x<=a)--->P(x<a+0.5)。

几何分布（Geometric Distribution）：用以描述n次独立的伯努利试验中试验x次才第一次成功的概率。

假如每次伯努利实验成功的概率为p，失败的概率为q=1-p，那么n次独立的伯努利实验中试验x次才第一次成功的概率是：。

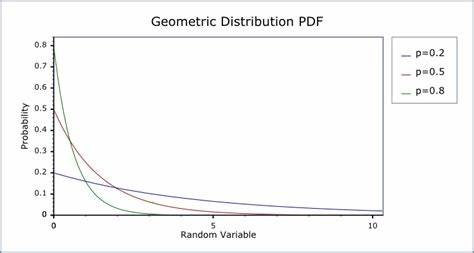
几何分布的期望：E(x)=1/p

几何分布的方差：Var(x)=q/p²

超几何分布（Hypergeometric Distribution）：用以描述从有限个（N个）物件中抽出n个物件（不放回），其中抽出k个指定种类物件的概率。

假如有N个物品，其中K个是某个特定种类，从这N个物品中抽出n个，其中k个是K种物品的概率是：。

超几何分布的期望：

超几何分布的方差：

最常见的超几何分布问题就是抽取卡牌：一副卡片共有20张，其中6张是红色的，14张是黑色的。从这20张卡片中随机抽取5张，其中4张是红色卡片的概率是多少？

当时，

当时，超几何分布的期望和二项分布的方差相同：

当时，超几何分布的方差和二项分布的方差相同：

当时，超几何分布近似为二项分布。

当n=1时，超几何分布还原为伯努利分布。

多项分布（Multinomial Distribution）：用以描述n次独立试验中有n_x次出现结果x的概率。

伯努利实验每次都只有2个可能的结果，若将其扩展为x个可能的结果，将该独立试验重复n次，那么出现n₁次p₁，n₂次p₂，...，n_x次p_x结果的概率是：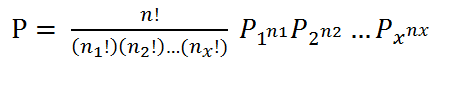

其中：

• n是试验的次数
• n₁是出现结果1的次数
• n₂是出现结果2的次数
• n_x是出现结果x的次数
• p₁是结果1出现的概率
• p₂是结果2出现的概率
• p_x是结果x出现的概率
• p_i>0，p₁+p₂+...+p_x=1

最常见的多项分布问题就是多次投骰子：投掷10次均匀的骰子，1次结果是6点，4次结果是4点，5次结果是2点的概率是多少？

多项分布和二项分布的区别在于：二项分布试验每次只有2个结果，而多项分布试验每次可以有多个结果。

均匀分布（Uniform Distribution）：随机变量在等长度的区间上取值的概率是相同的。

例如：投掷一颗均匀的骰子，每一面出现的概率都相同。

概率密度函数：（a≤x≤b）

均匀分布的期望：E(X) = (1/2)(a + b)

均匀分布的方差：Var(x) = (1/12)(b-a)²

泊松分布（Poisson Distribution）：用以描述在某个时间或空间范围内，某事件发生x次的概率。

其概率质量函数为：。（其中x是在某个时间或空间范围内事件发生的次数，λ是事件发生的平均次数）

泊松分布的期望：λ

泊松分布的方差：λ

最常见的泊松分布问题就是计算单位时间内经过某地的车辆数，或者单位时间内经过某地n辆车的概率。以公交车为例，假设我们知道它过去每个小时平均会5次经过其中一个站点（λ=5），那么它接下来一个小时经过该站点1次，4次，5次，10次的概率分别是多少？

• 当x=1时：P(1)=e⁻⁵5¹/1!≈0.034

• 当x=4时：P(4)=e⁻⁵5⁴/4!≈0.175

• 当x=5时：P(5)=e⁻⁵5⁵/5!≈0.175

• 当x=10时：P(10)=e⁻⁵5¹⁰/10!≈0.018

当λ>5时，泊松分布可以转换成正态分布。但是由于正态分布是连续变量，所以需要加一个continuity correction。

指数分布（Exponential Distribution）：用以描述泊松过程中随机事件发生的时间间隔的概率。泊松过程即事件以恒定的平均速率连续且独立地发生的过程。

例如：等公交车，两辆车到来的时间间隔，就符合指数分布。

其概率密度函数是：F(x) = λe ^{− λx}（x≥0，λ>0）（λ是单位时间事件发生的次数，x是事件发生的时间间隔）

其累积分布函数是：F(x) = 1 − e ^{− λx}（x ≥ 0; λ > 0） --- 表示在某个时间间隔内事件发生的概率（如果要表示在某个时间间隔内事件未发生的概率，则用1-F(x)=e ^{− λx}）

指数分布的期望：1/λ

指数分布的方差：1/λ²

指数分布主要用于测试产品可靠性。例如：某电视机厂生产的电视机平均10年出现1次大故障，且故障发生的次数服从泊松分布。求该电视机使用15年后还没有出现大故障的概率？

指数分布是无记忆性的。你等待的时间越长，事件发生的概率并不会发生改变。例如：某地发生了一次水灾，那么该地区在接下来一周，或十年以后发生水灾的概率是一样的。

总结如下：

	几何分布	二项分布	指数分布	超几何分布	泊松分布
概率分布类型	离散型概率分布	离散型概率分布	连续型概率分布	离散型概率分布	离散型概率分布
实验要求	每次实验是独立的。 每次实验只有成功和失败两种结果。 每次实验成功的概率是一样的。	实验次数是有限的。 每次实验是独立的。 每次实验只有成功和失败两种结果。 每次实验成功的概率是一样的。	在任意两个相等长度的区间上，事件发生的概率相等。 事件在某一区间上是否发生是独立的，与事件在其他区间上是否发生无关。	实验次数是有限的。 每次实验不独立。 每次实验只有成功和失败两种结果。 每次实验成功的概率都不同。	在任意两个相等长度的区间上，事件发生的概率相等。 事件在某一区间上是否发生是独立的，与事件在其他区间上是否发生无关。
随机变量	获得第一次成功的试验次数	试验成功的次数	事件发生的时间间隔	抽取指定种类物件的个数	在某个时间或空间范围内，某事件发生的次数
概率密度函数 或 概率质量函数			F(x) = λe − λx（x≥0，λ>0）
应用	进行n次独立的伯努利试验，求试验x次才第一次成功的概率	进行n次独立的伯努利实验，求x次成功的概率	已知单位时间内事件发生次数，求一段时间间隔内发生该事件的概率	从有限个（N个）物件中抽出n个物件（不放回），求其中抽出k个指定种类物件的概率	已知单位时间或空间内某事件发生的平均概率，求一段时间内发生x次该事件的概率或求一段时间内发生该事件的次数