MySQL(四）InnoDB中一棵B+树能存多少行数据

一、InnoDB一棵B+树可以存放多少行数据？(约2千万)

我们都知道计算机在存储数据的时候，有最小存储单元，这就好比我们今天进行现金的流通最小单位是一毛。在计算机中磁盘存储数据最小单元是扇区，一个扇区的大小是512字节，而文件系统（例如XFS/EXT4）他的最小单元是块，一个块的大小是4k，而对于我们的InnoDB存储引擎也有自己的最小储存单元——页（Page），一个页的大小是16K。

磁盘扇区、文件系统、InnoDB存储引擎都有各自的最小存储单元。

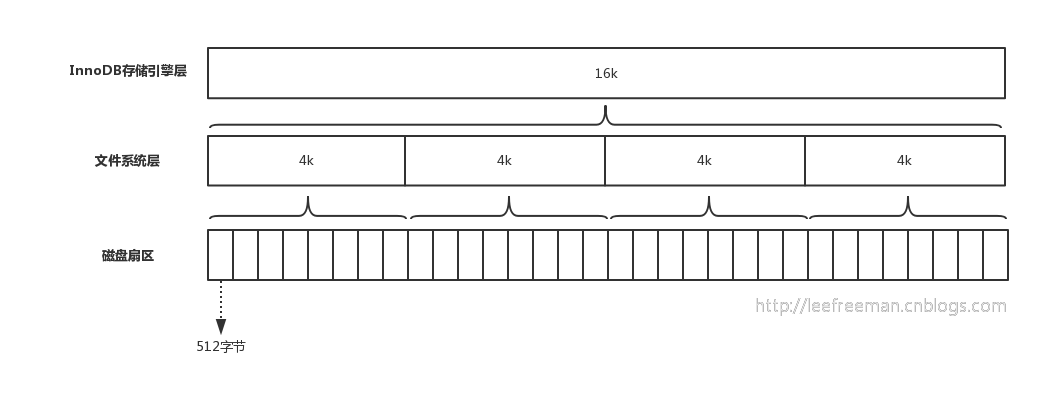
在MySQL中我们的InnoDB页的大小默认是16k，当然也可以通过参数设置：
SHOW VARIABLES LIKE 'innodb_page_size';

数据表中的数据都是存储在页中的，所以一个页中能存储多少行数据呢？

假设一行数据的大小是1k，那么一个页可以存放16行这样的数据。

用B+树的方式组织这些数据。如图所示：

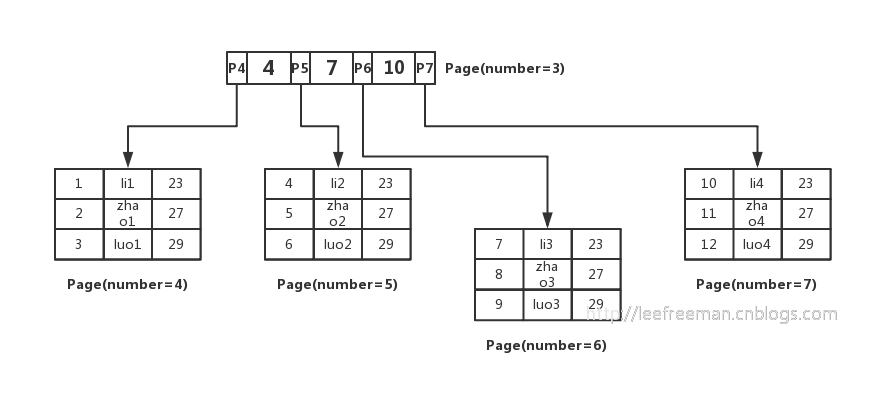
我们先将数据记录按主键进行排序，分别存放在不同的页中（为了便于理解我们这里一个页中只存放3条记录，实际情况可以存放很多），除了存放数据的页以外，还有存放键值+指针的页，如图中page number=3的页，该页存放键值和指向数据页的指针，这样的页由N个键值+指针组成。当然它也是排好序的。这样的数据组织形式，我们称为索引组织表。

现在来看下，要查找一条数据，怎么查？如select * from user where id=5;

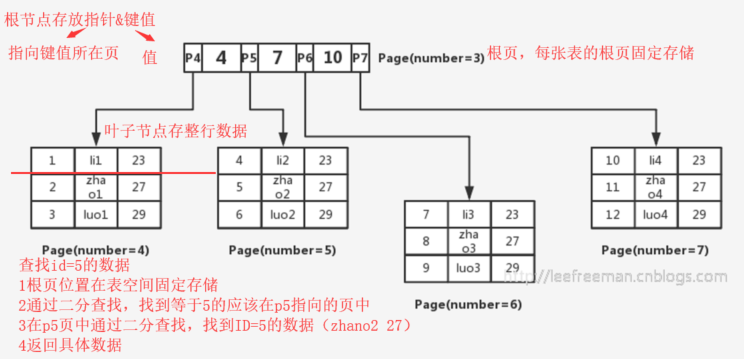
这里id是主键,我们通过这棵B+树来查找

1首先找到根页，你怎么知道user表的根页在哪呢？其实每张表的根页位置在表空间文件中是固定的，即page number=3的页，

2通过二分查找法，定位到id=5的数据应该在指针P5指向的页中，

3去page number=5的页中查找，同样通过二分查询法即可找到id=5的记录：

| 5 | zhao2 | 27 |

现在我们清楚了InnoDB中主键索引B+树是如何组织数据、查询数据的，我们总结一下：

1、InnoDB存储引擎的最小存储单元是页，页可以用于存放数据也可以用于存放键值+指针，在B+树中叶子节点存放数据，非叶子节点存放键值+指针。

2、索引组织表通过非叶子节点的二分查找法以及指针确定数据在哪个页中，进而在去数据页中查找到需要的数据；

二、通常一棵B+树可以存放多少行数据？

这里我们先假设B+树高为2，即存在一个根节点和若干个叶子节点，那么这棵B+树的存放总记录数为：根节点指针数*单个叶子节点记录行数。

上文我们已经说明单个叶子节点（页）中的记录数=16K（一页16KB）/1K（假设一行1KB）=16。（这里假设一行记录的数据大小为1k）。

那么现在我们需要计算出非叶子节点能存放多少指针？

其实这也很好算，我们假设主键ID为bigint类型，长度为8字节，而指针大小在InnoDB源码中设置为6字节，这样一共14字节，我们一个页中能存放多少这样的单元，其实就代表有多少指针，即16KB（16*1024=16384 byte）16384/14=1170（索引个数）。那么可以算出一棵高度为2的B+树，能存放1170*16=18720条这样的数据记录。

根据同样的原理我们可以算出一个高度为3的B+树可以存放：1170（索引个数）*1170（索引个数）*16（每页行数）=21902400（2千万）条这样的记录。

所以在InnoDB中B+树高度一般为1-3层，它就能满足千万级的数据存储。在查找数据时一次页的查找代表一次IO，所以通过主键索引查询通常只需要1-3次IO操作即可查找到数据。

四、怎么得到InnoDB主键索引B+树的高度？

上面我们通过推断得出B+树的高度通常是1-3，下面我们从另外一个侧面证明这个结论。在InnoDB的表空间文件中，约定page number为3的代表主键索引的根页，而在根页偏移量为64的地方存放了该B+树的page level。如果page level为1，树高为2，page level为2，则树高为3。即B+树的高度=page level+1；下面我们将从实际环境中尝试找到这个page level。

SELECT

  b.name,

  a.name,

  index_id,

  TYPE,

  a.`SPACE`,

  a.`PAGE_NO`

FROM

  information_schema.`INNODB_SYS_INDEXES` a,

  information_schema.`INNODB_SYS_TABLES` b

WHERE a.`TABLE_ID` = b.table_id

  AND a.`SPACE` <> 0

  AND b.`NAME` = 'testdts/mycity'

可以看出数据库testdts下的mycity表、mycity表主键索引根页的page number均为3，而其他的二级索引page number为4。

B+树高度为page level+1=3；region表的page level为0，B+树高度为page level+1=1；customer表的page level为2，B+树高度为page level+1=3；