bzoj 1001 原图最小割转化为对偶图最短路

题目大意：

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，

而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路 

1:(x,y)<==>(x+1,y) 

2:(x,y)<==>(x,y+1) 

3:(x,y)<==>(x+1,y+1) 

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，

开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，狼王开始伏击

这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，

才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的

狼的数量要最小。因为狼还要去找喜羊羊麻烦.

Input

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值. 

第二部分共N-1行，每行M个数，表示纵向道路的权值. 

第三部分共N-1行，每行M-1个数，表示斜向道路的权值. 

输入文件保证不超过10M

Output

输出一个整数，表示参与伏击的狼的最小数量.

Sample Input

3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6

Sample Output

14

基本思路：

据说Dicnic会被卡，据说剪枝一下就过了，蒟蒻表示根本不理解dicnic，

所以还是想直接上更快的sap算法，虽然理解的也不是恨透，但今天来不及了，明天再提交一次；

所以还是最小割转对偶图最短路，详见周冬的论文<<浅析最大最小定理在信息学竞赛中的应用>>

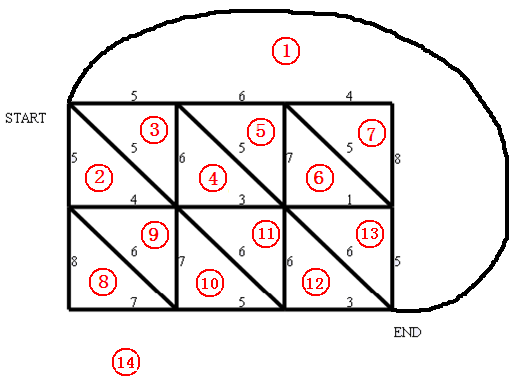
对偶图就是在原图中标号，然后找规律构造，如上图（借用了其他人的图）；

我不知道如果不是这种规则的图，还能不能构造出对偶图，个人觉得不行；

这样堆优化的dijkstra的时间复杂度就是O(nlogn)

代码如下：

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<string>
#include<algorithm>
#include<queue>
#include<vector>
 
using namespace std;
 
typedef long long ll;
typedef long long LL;
typedef pair<int,int> pii;
const int inf = 0x3f3f3f3f;
const int maxn = 1000000;
const ll mod = 1e9+9;
int n,m,num,cnt;
struct Edge{
    int v,w,next;
}edge[6*maxn+100];
int head[2*maxn+100],dis[2*maxn+100];
bool vis[2*maxn+100];
struct Node{
    int v,w;
    Node(int _v,int _w):v(_v),w(_w) {}
    bool operator<(const Node& a)const{
        return w>a.w;
    }
};
void addEdge(int u,int v,int w){
    edge[cnt].v=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void dijkstra(int s){
    memset(vis,false,sizeof(vis));
    memset(dis,inf,sizeof(dis));
    dis[s]=0;
    Node tmp(s,0);
    priority_queue<Node>pq;
    pq.push(tmp);
    while(!pq.empty()){
        tmp=pq.top();
        pq.pop();
        int u=tmp.v;
        if(vis[u]){
            continue;
        }
        vis[u]=true;
        for(int i=head[u];i!=-1;i=edge[i].next){
            int v=edge[i].v;
            int w=edge[i].w;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                pq.push(Node(v,dis[v]));
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    if(n==1||m==1){
        int ans=inf;
        int _max=max(n,m);
        for(int i=1;i<_max;i++){
            int u;
            scanf("%d",&u);
            ans=min(ans,u);
        }
        printf("%d\n",ans);
        return 0;
    }
    cnt=0;
    memset(head,-1,sizeof(head));
    int u,v,w;
    for(int i=1;i<=n;i++){
        for(int j=1;j<m;j++){
            scanf("%d",&w);
            if(i==1){
                u=1;
                v=j*2+1;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }else if(i==n){
                u=(n-1)*(m-1)*2+2;
                v=((i-2)*(m-1)+j)*2;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }else{
                u=((i-2)*(m-1)+j)*2;
                v=((i-1)*(m-1)+j)*2+1;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }
        }
    }
    for(int i=1;i<n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&w);
            if(j==1){
                u=(n-1)*(m-1)*2+2;
                v=((i-1)*(m-1)+j)*2;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }else if(j==m){
                u=1;
                v=((i-1)*(m-1)+j-1)*2+1;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }else{
                u=((i-1)*(m-1)+j-1)*2+1;
                v=((i-1)*(m-1)+j)*2;
                addEdge(u,v,w);
                addEdge(v,u,w);
            }
        }
    }
    for(int i=1;i<n;i++){
        for(int j=1;j<m;j++){
            scanf("%d",&w);
            u=((i-1)*(m-1)+j)*2;
            v=((i-1)*(m-1)+j)*2+1;
            addEdge(u,v,w);
            addEdge(v,u,w);
        }
    }
    num=(n-1)*(m-1)*2+2;
    dijkstra(1);
    printf("%d\n",dis[num]);
    return 0;
}