[CSP-S模拟测试]:字符消除2（hash+KMP）

题目背景

生牛哥终于打通了“字符消除”，可是他又被它的续集难倒了。

---

题目传送门（内部题52）

---

输入格式

第一行$n$表示数据组书。
接下来每行一个字符串。（只包含大写字母）

---

输出格式

每组数据输出一个$01$串。

---

样例

样例输入：

3
YDYYDY
JRYJREJRYJR
YDYAKYDY

样例输出：

010010
01001101001
01000010

---

数据范围与提示

---

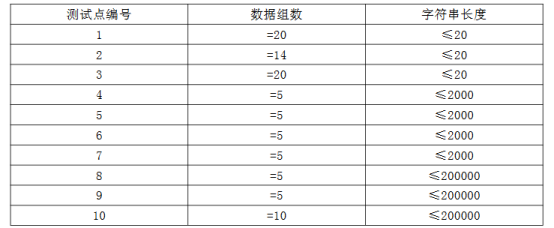
题解

为方便，我们设串长为$S$。

首先，来解释一下什么是可行$t$。

对于样例中的第一个串$"YDYYDY"$，我看它比较帅，所以就拿它举例。

它的可行$t$集合为$3$和$6$，为什么呢？

对于一个长度为$3$的环，我们可以这么填：

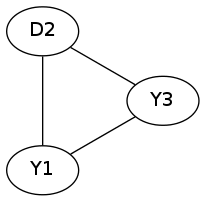
这时，我们填成了一圈，然后我们去填第二圈：

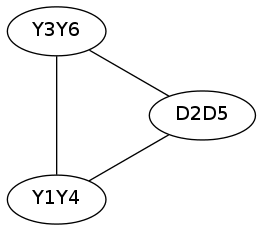
刚好填完，所以它是一个可行$t$，长度为$6$时同理，可是当长度为$4$当我们填到第五个$D$时发现那个位置已经填了$Y$，所以就不可行了。

题意解释完了，我们现在开始考虑这道题应该怎么办？

先来考虑如何求出可行$t$的集合。

我们发现，如果这个串有一个长度为$len$的公共前后缀，那么其中一个可行$t$就是$len-1$，来解释一下：

对于一个公共前后缀，如下图：

橙色区域是公共前后缀，绿色区域是串，显然$a\sim b$点即为长度$len$，那么当我们处理到$c$点时完成了一个环，但是接下来我们要填的$c\sim d$这部分和$a\sim b$是一样的，所以这个$n-len$就是一个长度$t$。

对于$t$的集合，我们可以通过$hash$或者是$KMP$在$\Theta(S)$的时间复杂度内求出。

虽说我用的是$hash$，但是我想讲一下$KMP$如何求出，我们只需要从$n$向前不断的找$next$就好了，也就是$next[next[i]]$，下面来解释为什么：

设橙色区域即$a\sim d$是$next[n]$，也就是说$1-$橙色区域是一组可行$t$，现在另紫色区域即$a\sim b$是$next[next[n]]$，现在来证明$1-$紫色区域是一组可行$t$：

　　因为$a\sim d$和$e\sim h$相同，$a\sim b$、$c\sim d$、$e\sim f$、$g\sim h$相同，所以我们可以当填一圈填到$g$时接着填完最后$g\sim h$（$a\sim b=g\sim h$）。

现在再来考虑如何生成$01$串，显然枚举是不可能的。

设$a$数组表示所有的公共前后缀集合（其实就是$KMP$中的$next$数组），注意不是可行$t$，那么这时候分两种情况：

　　$\alpha.a[k]\times 2\geqslant a[k+1]$：这时候我们就将$01$串后面接上一段长度为$a[k+1]-a[k]$的后缀即可，如下图：

　　

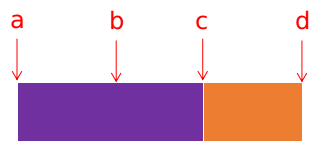
　　我们现在已经处理好了$a\sim c$这一段，现在要将填$c\sim d$这一段，不妨另$len(b\sim c)=len(c\sim d)$注意现在$c$是$next[d]$，也就是说我们要使$a\sim c=b\sim d$，那么显然是要将$b\sim c$复制到$c\sim d$。

　　$\beta.a[k]\times 2<a[k+1]$：考虑$next$数组的含义，为了保证解最优，我们一定是先将整个串复制一遍放在最后，然后在中间先填满$0$，如果不行的话将最后一个$0$换成$1$即可，至于如何判断，暴力搞就好了，因为如果$0$不行的话最后以为是$1$肯定行。

这样我们就完美的解决了这道题。

时间复杂度：$\Theta(\sum S)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n;
char ch[200001];
int b[200001],que[200001],nxt[200001],p;
unsigned long long a[200001],mod[200001];
void pre_work()
{
	memset(nxt,0,sizeof(nxt));
	memset(b,0,sizeof(b));
	p=que[0]=0;
}
void KMP(int l,int r)
{
	for(int i=l+1;i<=r;i++)
	{
		while(p&&b[i]!=b[p+1])p=nxt[p];
		if(b[i]==b[p+1])p++;
		nxt[i]=p;
	}
}
int main()
{
	int T;scanf("%d",&T);
	mod[1]=1;
	for(int i=2;i<=200000;i++)mod[i]=mod[i-1]*131;
	while(T--)
	{
		scanf("%s",ch+1);
		pre_work();
		n=strlen(ch+1);
		a[1]=ch[1]-'A'+1;
		for(int i=2;i<=n;i++)
			a[i]=a[i-1]*131+ch[i]-'A'+1;
		for(int i=0;i<=n;i++)
			if(a[i+1]==a[n]-a[n-i-1]*mod[i+2])que[++que[0]]=i+1;
		if(que[1]>1)b[que[1]]=1;
		KMP(1,que[1]);
		for(int i=2;i<=que[0];i++)
		{
			if(que[i]<=que[i-1]<<1)
			{
				for(int j=que[i-1]+1;j<=que[i];j++)
					b[j]=b[j+que[i-1]-que[i]];
				KMP(que[i-1],que[i]);
			}
			else
			{
				KMP(que[i-1],que[i]-que[i-1]-1);
				int now=p,zero=1,len=que[i]-que[i-1];
				while(now)
				{
					if(!b[now+1]&&!(len%(len-now-1))){b[len]=1;break;}
					now=nxt[now];
				}
				if(!b[now+1]&&!(len%(len-now-1)))b[len]=1;
				KMP(len-1,len);
				nxt[len]=p;
				len=que[i]-que[i-1];
				for(int j=1;j<=que[i-1];j++)b[len+j]=b[j];
				KMP(len,len+que[i-1]);
			}
		}
		for(int i=1;i<=n;i++)printf("%d",b[i]);
		puts("");
	}
	return 0;
}

---

rp++