剑指offer--day03

1.1题目：斐波那契数列：大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。n<=39

1.2解题思路：斐波那契数列公式为：

　　这道题递归很好写，但是存在很严重的效率问题。我们以求解f(10)为例类分析递归的求解过程。想求f(10)，需要先求得f(9)和f(8)。同样，想求得f(9)，需要先求的f(8)和f(7)....我们可以用树形结构来表示这种依赖关系，如下图所示：

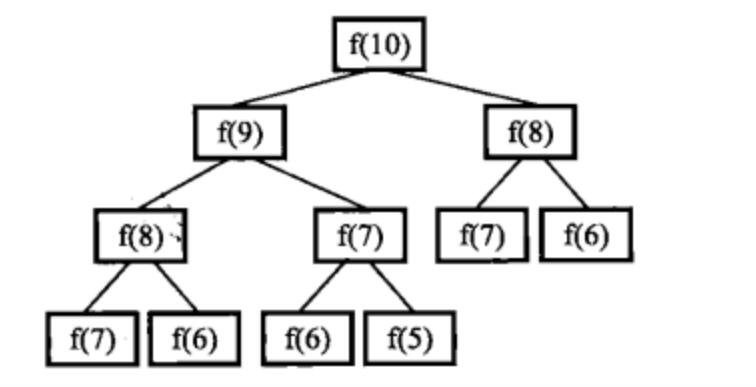
　　我们不难发现在这棵树中有很多结点是重复的，而且重复的结点数会随着n的增加而急剧增加，这意味计算量会随着n的增加而急剧增大。事实上，递归方法计算的时间复杂度是以n的指数的方式递增的。

　　所以，使用简单的循环方法来实现。

1.3代码：

 # -*- coding:utf-8 -*-
 class Solution:
     def Fibonacci(self, n):
         # write code here
         if n <= 1:
             return n
         first = 0
         second = 1
         f = 0
         for i in range(2, n+1):
             f = first + second
             first = second
             second = f
         return f

2.1题目：跳台阶：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

2.2解题思路：

　　首先我们考虑最简单的情况。如果只有1级台阶，那么显然只一种跳法。如果有2级台阶，那就有两种跳法：一种是分两次跳，每次跳1级；另一种是一次跳2级。

　　接着，我们来讨论一般情况。我们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是跳一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里，我们不难看出这实际上就是斐波那契数列了。

2.3代码：

 class Solution:
     def jumpFloor(self, number):
         # write code here
         if number <= 2:
             return number
         first = 1
         second = 2
         f = 0
         for i in range(3, number+1):
             f = first + second
             first = second
             second = f
         return f

刷题平台：牛客网：https://www.nowcoder.com/ta/coding-interviews

参考：https://cuijiahua.com/