Gorgeous Sequence（线段树）

Gorgeous Sequence

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 6946    Accepted Submission(s): 1784

Problem Description

There is a sequence a of length n. We use ai to denote the i-th element in this sequence. You should do the following three types of operations to this sequence.

0 x y t: For every x≤i≤y, we use min(ai,t) to replace the original ai's value.
1 x y: Print the maximum value of ai that x≤i≤y.
2 x y: Print the sum of ai that x≤i≤y.

 

Input

The first line of the input is a single integer T, indicating the number of testcases.

The first line contains two integers n and m denoting the length of the sequence and the number of operations.

The second line contains n separated integers a1,…,an (∀1≤i≤n,0≤ai<231).

Each of the following m lines represents one operation (1≤x≤y≤n,0≤t<231).

It is guaranteed that T=100, ∑n≤1000000, ∑m≤1000000.

 

Output

For every operation of type 1 or 2, print one line containing the answer to the corresponding query.

 

Sample Input

1
5 5
1 2 3 4 5
1 1 5
2 1 5
0 3 5 3
1 1 5
2 1 5

 

Sample Output

5
15
3
12

Hint

Please use efficient IO method

 

Author

XJZX

 

Source

2015 Multi-University Training Contest 2

 

Recommend

wange2014   |   We have carefully selected several similar problems for you:  6554 6553 6552 6551 6550 

题意 ：

有一个长度为n的序列a。我们用ai来表示这个序列中的第i个元素。您应该对这个序列执行以下三种类型的操作。

0 x y t:对于每一个x≤i≤y，我们用min(ai,t)替换原始ai的值。

1 x y:打印ai的最大值，即x≤i≤y。

2xy:输出x≤i≤y的ai之和。

输入

输入的第一行是一个整数T，表示测试用例的数量。

第一行包含两个整数n和m，表示序列的长度和操作的数量。

第二行包含n分离整数a1,…,一个(∀1≤≤n, 0≤ai < 231)。

以下m行每一行表示一个操作(1≤x≤y≤n,0≤t<231)。

保证T=100，∑n≤1000000，∑m≤1000000。

输出

对于类型1或2的每个操作，打印一行包含相应查询的答案。

题解：

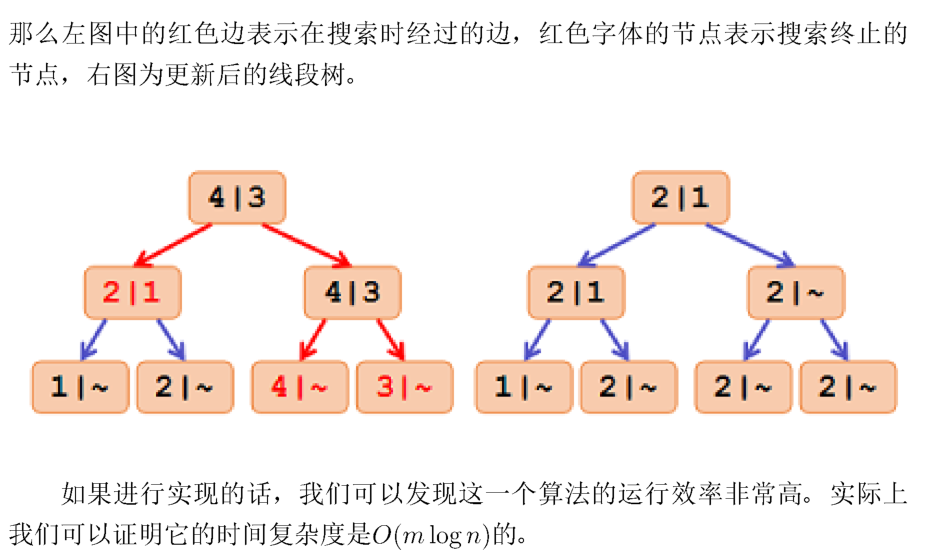
c++代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + ;
int a[maxn];
#define EF if(ch==EOF) return x;
// #define lc k<<1
// #define rc k<<1|1
inline int read(){
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;EF;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
struct tree
{
    int l , r;
    int miax , maxx;
    ll sum;
    int set_lazy;
}t[maxn << ];

// inline void push_up(int k){
//     // sum[k]=sum[lc]+sum[rc];
//     // mx[k]=max(mx[lc],mx[rc]);
//     // se[k]=max(se[lc],se[rc]);
//     // mc[k]=0;
//     // if(mx[lc]!=mx[rc]) se[k]=max(se[k],min(mx[lc],mx[rc]));
//     // if(mx[k]==mx[lc]) mc[k]+=mc[lc];
//     // if(mx[k]==mx[rc]) mc[k]+=mc[rc];
//     t[k].sum = t[lc].sum + t[rc].sum;
//     t[k].maxx = max(t[lc].maxx,t[rc].maxx);
//     t[k].miax = max(t[lc].miax,t[rc].miax);
//     t[k].set_lazy = 0;
//     if(t[lc].maxx != t[rc].maxx) t[k].miax = max(t[k].miax,min(t[lc].maxx,t[rc].maxx));
//     if(t[k].maxx == t[lc].maxx) t[k].set_lazy += t[lc].set_lazy;
//     if(t[k].maxx == t[rc].maxx) t[k].set_lazy += t[rc].set_lazy;

// }
inline void push_up(int rt){
    t[rt].sum = t[rt << ].sum + t[rt << |].sum;
   // t[rt].minn = min(t[rt << 1].minn,t[rt << 1|1].minn);
    t[rt].maxx = max(t[rt << ].maxx,t[rt << |].maxx);
    t[rt].miax = max(t[rt << ].miax, t[rt << |].miax);
    t[rt].set_lazy = ;
    if(t[rt << ].maxx != t[rt <<|].maxx) t[rt].miax = max(t[rt].miax,min(t[rt << ].maxx , t[rt <<|].maxx));
    //打上标记，记录下标记个数
    if(t[rt].maxx == t[rt << ].maxx) t[rt].set_lazy += t[rt << ].set_lazy;
    if(t[rt].maxx == t[rt << |].maxx) t[rt].set_lazy += t[rt << |].set_lazy;
   // cout << t[rt].sum << " " << rt <<endl;
}

inline void dec_tag(int rt,int v){
    if(v >= t[rt].maxx) return;
    t[rt].sum += 1ll * (v - t[rt].maxx)*t[rt].set_lazy;
    t[rt].maxx = v;
}

inline void push_down(int rt){
    dec_tag(rt << ,t[rt].maxx);
    dec_tag(rt << |,t[rt].maxx);
}
  // inline void push_down(int rt) {
  //       if(t[rt].set_lazy) { ///if set_lazy add_lazy = 0
  //           t[rt<<1].set_lazy = t[rt].set_lazy;
  //           t[rt<<1].sum = (t[rt<<1].r - t[rt<<1].l + 1) * t[rt].set_lazy;
  //           t[rt<<1].maxx = t[rt].set_lazy;
  //           t[rt<<1].minn = t[rt].set_lazy;
  //           t[rt<<1|1].set_lazy = t[rt].set_lazy;
  //           t[rt<<1|1].sum = (t[rt<<1|1].r - t[rt<<1|1].l + 1) * t[rt].set_lazy;
  //           t[rt<<1|1].maxx = t[rt].set_lazy;
  //           t[rt<<1|1].minn = t[rt].set_lazy;
  //           //tre[rt].add_lazy = 0;
  //           //tre[rt<<1].add_lazy = tre[rt<<1|1].add_lazy = 0;
  //           t[rt].set_lazy = 0;
  //           return ;
  //       }
  //       // if(tre[rt].add_lazy) {
  //       //     tre[rt<<1].add_lazy += tre[rt].add_lazy;
  //       //     tre[rt<<1].sum += (tre[rt<<1].r - tre[rt<<1].l + 1) * tre[rt].add_lazy;
  //       //     tre[rt<<1].max += tre[rt].add_lazy;
  //       //     tre[rt<<1].min += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].add_lazy += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].sum += (tre[rt<<1|1].r - tre[rt<<1|1].l + 1) *
  //       //                         tre[rt].add_lazy;
  //       //     tre[rt<<1|1].max += tre[rt].add_lazy;
  //       //     tre[rt<<1|1].min += tre[rt].add_lazy;
  //       //     tre[rt].add_lazy = 0;
  //       // }
  //   }

void build(int rt,int l ,int r){
    t[rt].l = l, t[rt].r = r;
    //t[rt].set_lazy = 1;

    if(l == r){
        t[rt].sum =  t[rt].maxx = a[l];
        t[rt].miax = -;
        t[rt].set_lazy = ;
       // cout <<"nbb  " <<t[rt].sum << " "<<rt << endl;
        return;
    }
    int mid = (l + r) >> ;
    build(rt <<,l,mid);
    build(rt << |,mid + ,r);
    push_up(rt);
}

void up_date(int rt,int l,int r,int d){
    if(d >= t[rt].maxx) return;

    //push_down(rt);
    if(l <= t[rt].l && r >= t[rt].r && d > t[rt].miax){
     // t[rt].sum = (t[rt].r - t[rt].l + 1) * d;
     // t[rt].maxx = d;
     // t[rt].minn = d;
     // t[rt].set_lazy = d;
     dec_tag(rt,d);
     return;
 }
 push_down(rt);
 int mid = (t[rt].l + t[rt].r) >> ;
 if(r <= mid) {
    up_date(rt<<,l,r,d);
} else if(l > mid) {
    up_date(rt<<|,l,r,d);
} else {
    up_date(rt<<,l,mid,d);
    up_date(rt<<|,mid+,r,d);
}
push_up(rt);
}

 ll query_sum(int rt,int l,int r) { ///sum

    if(l <= t[rt].l && t[rt].r <= r) {
        return t[rt].sum;
    }
    push_down(rt);
    int mid = (t[rt].l + t[rt].r) >> ;
    if(r <= mid) {
        return query_sum(rt<<,l,r);
    } else if(l > mid) {
        return query_sum(rt<<|,l,r);
    } else {
        return query_sum(rt<<,l,mid) + query_sum(rt<<|,mid+,r);
    }
}

    int query_max(int rt,int l,int r) { ///max

       //cout << t[rt].maxx  << endl;
        if(l <= t[rt].l && t[rt].r <= r) {
            return t[rt].maxx;
        }
        push_down(rt);
        int mid = (t[rt].l + t[rt].r) >> ;
        if(r <= mid) {
            return query_max(rt<<,l,r);
        } else if(l > mid) {
            return query_max(rt<<|,l,r);
        } else {
            return max(query_max(rt<<,l,mid), query_max(rt<<|,mid+,r));
        }
    }
    // int query_min(int rt,int l,int r) { ///min
    //     push_down(rt);

    //     if(l <= t[rt].l && t[rt].r <= r) {
    //         return t[rt].minn;
    //     }
    //     int mid = (t[rt].l + t[rt].r) >> 1;
    //     if(r <= mid) {
    //         return query_min(rt<<1,l,r);
    //     } else if(l > mid) {
    //         return query_min(rt<<1|1,l,r);
    //     } else {
    //         return min(query_min(rt<<1,l,mid), query_min(rt<<1|1,mid+1,r));
    //     }
    // }

    int main(int argc, char const *argv[])
    {
        int t;
        //scanf("%d",&t);
        t = read();
        while(t--){
            int n , q;
            //scanf("%d%d",&n,&q);
            n = read(),q = read();
            for(int i = ;i <= n; i++) //scanf("%d",&a[i]);
                a[i] = read();
            build(,,n);
   // //0 cout << 1;
   //  for(int i = 1;i <= n; i++){
   //      cout << t[i].maxx ;
   //  }
            while(q--){
                int a,b,c;
                //scanf("%d%d%d",&a,&b,&c);
                a = read() ,b = read() , c = read();
                if(a == ){
                    int z;
                    //scanf("%d",&z);
                    z = read();

                    up_date(,b,c,z);
                }
                else if(a == ){
                    printf("%d\n",query_max(,b,c));
                }
                else{
                    printf("%lld\n",query_sum(,b,c));
                }
            }
        }
        return ;
    }