【6.24校内test】T2 不老梦

【题目背景】

于万人中万幸得以相逢，刹那间澈净明通。

成为我所向披靡的勇气和惶恐，裂山海，堕苍穹。

爱若执炬迎风，炽烈而哀恸，诸般滋味皆在其中。

韶华宛转吟诵，苍凉的光荣，急景凋年深情难共。

——银临《不老梦》

【问题描述】

扶苏翻遍了歌单却没有找到一首歌能做这个题的题目背景，于是放上了扶苏最喜欢 的一首《不老梦》。

与 Day1 的第二题一样，今天的第二题依然是一道树论题。（讨厌数论题没有之一！！）

我们定义一棵 n 个节点的树为一个有 n 个节点和 n-1 条边的无向连通图。

如果我们定义 u 是一颗树 T 的根，那么任意一个节点 v 到根的路径就是从 v 出发到 达点 u 的简单路径上所经过的点的点集。可以证明这样的简单路径有且仅有一条。

定义一个节点 x 是节点 y 的孩子，当且仅当 x 和 y 之间有边相连且 x 不在 y 到根的 路径中。如果 x 是 y 的孩子，那么定义 y 是 x 的家长节点。

如果我是 _rqy 那种毒瘤神仙的话，可能会问你每个节点的孩子数不超过 k 的 n 个节 点的带标号无根树一共有多少个，可惜这个问题我也不会，所以我不会问你这么毒瘤的 问题。

扶苏从一颗 n 个节点的树的 1 号节点出发，沿着树上的边行走。当然我们约定 1 号 节点是这棵树的根。他所行走的规定是：当扶苏在点 u 时，扶苏要么在 u 的孩子中选择 一个没有到达过得点 v 并行走到 v，要么选择回到 u的家长节点。

现在给每个节点一个权值 w，其中 i 号节点的权值为 wi。扶苏有一些石子，他想给 这棵树上的某一个节点放上石子。我们规定扶苏能在节点 u 放上石子当且仅当满足如下 条件：

1、扶苏当前在节点 u

2、对于 u 的所有孩子节点v，节点 v 被放上了 wv 颗石子。

但是，扶苏在任意时刻都可以取回任意节点的石子。

现在，扶苏想问问你对于每个节点，如果他想在 i 号节点上放 wi 颗石子，那么他一 开始需要准备多少石子。

【输入格式】

输入文件名为 yin.in。

输入文件中有且仅有一组数据，数据的第一行是一个整数 n 代表树的节点个数。

第二行有 n-1 个整数，第 i 个整数 pi 代表 i+1 号节点的家长节点的编号。

第三行有 n 个整数，第 i 个整数代表 wi。

【输出格式】

输出文件名为 yin.out。

输出一行 n 个整数，第 i 个整数代表想在 i 号节点上放 wi 颗石子需要准备的 石子个数。

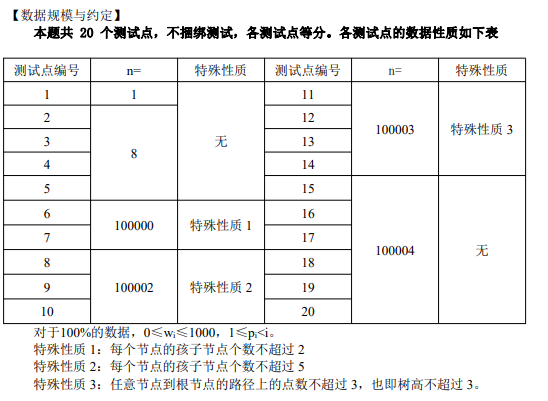
显然给了测试点的数据，我们就可以逐个击破：

【测试点1】这个显然没有任何的技术含量啦，直接输出w1就可以啦。5pts get√

【测试点2-5】爆搜，搜出一个放石子的顺序，然后 O(n) 的 check 是否合法。时间复杂度 O(n!n)。期望得分 20 分。（但是我不会写嘤嘤嘤(╥╯^╰╥)）

【测试点6-7】注意到根据题目规定的走法，在进入一个节点以后，必须遍历完它的整个子树， 否则一旦离开这个节点，再也无法进入这棵子树，从而导致该节点的某个孩子没能放 上石子，导致这个节点不能放上石子。同时又有每个节点放上石子以后，它的子树的 石子可以全部取回。设在节点 u 放石子需要有 ans_u 个石子，则放完 u 以后可以取回 ans_u-w_u 个石子。

于是考虑影响问题答案的显然是从 u 进入每个孩子的顺序，由于最多有两个孩 子，直接比较一下就可以知道先进入哪个孩子更优秀了。时间复杂度 O(n)，期望得分 10 分。

【测试点8-10】延续上一组测试点的思路，由于只有最多 5 个孩子，可以直接爆搜选孩子的顺 序，看看哪个更优秀。时间复杂度 O(n*x!)，其中 x=5。期望得分 15 分。

【测试点11-14】（正解前导论，划重点）

【测试点15-20】可以发现上面的结论同样适用于树高更高的情况，于是在 dfs 回溯的时候对子节 点排序，即可算出该节点的答案，期望得分 30 分。

好了以下是充满了ZAY风起的STD（不用指针会死zay）

#include <cstdio>
#include <vector>
#include <algorithm>

const int maxn = ;

int n;
int MU[maxn], ans[maxn];
std::vector<int>son[maxn];

void dfs(const int u);
bool cmp(const int &_a, const int &_b);

int main() {
  freopen("yin.in", "r", stdin);
  freopen("yin.out", "w", stdout);
  scanf("%d", &n);
  for (int i = , x; i <= n; ++i) {//直 接 i 从 2 开 始 枚 举，就 不 用 i+1 了
    scanf("%d", &x);
    son[x].push_back(i);//动 态 数 组 嘛 qwq
  }
  for (int i = ; i <= n; ++i) {
    scanf("%d", MU + i);//指 针 可 海 星
  }
  dfs();
  for (int i = ; i < n; ++i) {
    printf("%d ", ans[i]);
  }
  printf("%d\n", ans[n]);
  return ;
}

void dfs(const int u) {
  for (auto v : son[u]) {//遍历u结点的所有儿子，赋值给v
    dfs(v);//先遍历所有儿子，最后再操作1
  }
  std::sort(son[u].begin(), son[u].end(), cmp);//将u结点的所有儿子按照ansi-wi不升序排序
  int _ret = ;
  //此时u结点所有的e子的ans都已经计算出来了
  for (auto v : son[u]) {//对于叶子结点（没有e子），不进行这个for循环
  //对于其它结点，
    if (_ret >= ans[v]) {//显然由于遍历是有顺序的，当我们遍历到某些结点时，其之前遍历的
    //结点的石子和（除去结点u的e子），（显然除了u结点所对应的儿子结点v们，这些v的儿子上的石子都可以删除啦）
    //如果这些多出来的石子>某个未被遍历到的结点所需石子数，显然直接放过去就好了√
      _ret -= ans[v];//这样剩余的石子就减少啦
      //然后相当于ans[v]的贡献是0
    } else {
      ans[u] += ans[v] - _ret;//计算ans[u]：+它的e子结点所需要的石子-剩余石子
      _ret = ans[v] - MU[v];//表示遍历完u的e子v这个结点对应滴子树后，可以收回除了u的e子v以外所有结点上的石头
      //因此ret=ans[v]-MU[v]
    }
  }
  ans[u] += std::max(, MU[u] - _ret);
  //对于叶节点，ans[u]=0；
  //对于其它结点
}

inline bool cmp(const int &_a, const int &_b) {
  return (ans[_a] - MU[_a]) > (ans[_b] - MU[_b]);//按照ansi-wi不升序排序
}

end-