洛谷P1174 打砖块

题目描述

小红很喜欢玩一个叫打砖块的游戏，这个游戏的规则如下：

在刚开始的时候，有n行*m列的砖块，小红有k发子弹。小红每次可以用一发子弹，打碎某一列当前处于这一列最下面的那块砖，并且得到相应的得分。(如图所示)

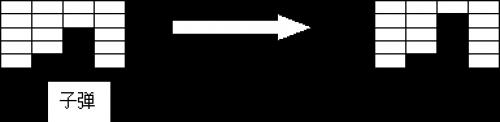
某些砖块在打碎以后，还可能将得到一发子弹的奖励。最后当所有的砖块都打碎了，或者小红没有子弹了，游戏结束。

小红在游戏开始之前，就已经知道每一块砖在打碎以后的得分，并且知道能不能得到一发奖励的子弹。小红想知道在这次游戏中她可能的最大得分，可是这个问题对于她来说太难了，你能帮帮她吗？

输入输出格式

输入格式：

第一行有3个正整数，n，m，k。表示开始的时候，有n行*m列的砖块，小红有k发子弹。

接下来有n行，每行的格式如下：

f1 c1 f2 c2 f3 c3 …… fm cm

其中fi为正整数，表示这一行的第i列的砖，在打碎以后的得分。ci为一个字符，只有两种可能，Y或者N。Y表示有一发奖励的子弹，N表示没有。

所有的数与字符之间用一个空格隔开，行末没有多余的空格。

输出格式：

仅一个正整数，表示最大的得分。

输入输出样例

输入样例#1：

3 4 2
9 N 5 N 1 N 8 N
5 N 5 Y 5 N 5 N
6 N 2 N 4 N 3 N

输出样例#1：

13

说明

对于20%的数据，满足1<=n,m<=5，1<=k<=10，所有的字符c都为N

对于50%的数据，满足1<=n,m<=200，1<=k<=200，所有的字符c都为N

对于100%的数据，满足1<=n,m<=200，1<=k<=200，字符c可能为Y

对于100%的数据，所有的f值满足1<=f<=10000

如果没有奖励子弹的话，相当于一个分组背包，决策每一列打几个就可以了。

↑50分解法

有奖励子弹的话，就有了特殊情况：例如某一列最下面有x个普通方块，其上面有一串奖励方块，要想拿到奖励方块，必须得预留x+1颗子弹，这多出来的1颗子弹可以在以后用来打之前某列的砖块。

所以需要多一维状态，处理留一发子弹/不留的情况。

状态多了有些迷茫，半抄着题解写完……我已经是条咸鱼了。

f1是留一发子弹的状态，f2是都打完的状态。

 /*by SilverN*/
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<vector>
 using namespace std;
 const int mxn=;
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<'' || ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>='' && ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int f1[mxn][mxn],f2[mxn][mxn];//[列][使用子弹数]=最优解
 int n,m,k;
 int mp[mxn][mxn];
 bool re[mxn][mxn];
 int w1[mxn][mxn],w2[mxn][mxn];
 void init(){
     for(int j=;j<=m;j++){
         int cnt=n;
         while(cnt && re[cnt][j]){
             w1[j][]+=mp[cnt][j];
             cnt--;
         }
         for(int i=;i<=n && cnt ;i++){//打了i发子弹
             w2[j][i]=w1[j][i-]+mp[cnt][j];
             w1[j][i]=w2[j][i];
             cnt--;
             while(cnt && re[cnt][j]){
                 w1[j][i]+=mp[cnt][j];
                 cnt--;
             }
         }
     }
     return;
 }
 int main(){
     n=read();m=read();k=read();
     int i,j;
     for(i=;i<=n;i++)
      for(j=;j<=m;j++){
          mp[i][j]=read();
          char ch=getchar();
          if(ch=='N')re[i][j]=;
          else re[i][j]=;
      }
     init();
     /*
     for(i=1;i<=n;i++){
      for(j=1;j<=m;j++){
          printf("%5d %5d ",mp[i][j],num[i][j]);
      }
      printf("\n");
     }*/
     for(i=;i<=m;i++){//列
         for(j=;j<=k;j++){//子弹
             for(int l=;l<=j;l++){//之前已用子弹
                 f1[i][j]=max(f1[i][j],f1[i-][j-l]+w1[i][l]);
                 if(l<j){
                     f2[i][j]=max(f2[i][j],f2[i-][j-l]+w1[i][l]);
                 }
                 if(l){
                     f2[i][j]=max(f2[i][j],f1[i-][j-l]+w2[i][l]);
                 }
             }
         }
     }
     printf("%d\n",f2[m][k]);
     return ;
 }