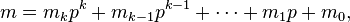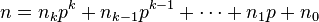lucas定理,组合数学问题
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。
这里用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
代码:

typedef long long LL;
using namespace std; LL exp_mod(LL a, LL b, LL p) {
LL res = 1;
while(b != 0) {
if(b&1) res = (res * a) % p;
a = (a*a) % p;
b >>= 1;
}
return res;
} LL Comb(LL a, LL b, LL p) {
if(a < b) return 0;
if(a == b) return 1;
if(b > a - b) b = a - b; LL ans = 1, ca = 1, cb = 1;
for(LL i = 0; i < b; ++i) {
ca = (ca * (a - i))%p;
cb = (cb * (b - i))%p;
}
ans = (ca*exp_mod(cb, p - 2, p)) % p;
return ans;
} LL Lucas(int n, int m, int p) {
LL ans = 1; while(n&&m&&ans) {
ans = (ans*Comb(n%p, m%p, p)) % p;
n /= p;
m /= p;
}
return ans;
} int main() {
Read();
int n, m, p;
while(~scanf("%d%d%d", &n, &m, &p)) {
printf("%lld\n", Lucas(n, m, p));
}
return 0;
}

lucas定理,组合数学问题的更多相关文章
- Bzoj 4403: 序列统计 Lucas定理,组合数学,数论
4403: 序列统计 Time Limit: 3 Sec Memory Limit: 128 MBSubmit: 328 Solved: 162[Submit][Status][Discuss] ...
- BZOJ4403: 序列统计【lucas定理+组合数学】
Description 给定三个正整数N.L和R,统计长度在1到N之间,元素大小都在L到R之间的单调不降序列的数量.输出答案对10^6+3取模的结果. Input 输入第一行包含一个整数T,表示数据组 ...
- HDU 5226 Tom and matrix(组合数学+Lucas定理)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5226 题意:给一个矩阵a,a[i][j] = C(i,j)(i>=j) or 0(i < ...
- lucas定理和组合数学
自湖南长沙培训以来的坑...一直未填,今天把这个问题解决掉. 参考: 1.http://www.cnblogs.com/Var123/p/5523068.html 2.http://blog.csdn ...
- Lucas定理及应用
额,前两天刚讲了数据结构,今天我来讲讲组合数学中的一种奇妙优化——Lucas 先看这样一个东西 没学过lucas的肯定会说:还不简单?处理逆元,边乘边膜呗 是,可以,但注意一下数据范围 你算这一次,你 ...
- [学习笔记]扩展LUCAS定理
可以先做这个题[SDOI2010]古代猪文 此算法和LUCAS定理没有半毛钱关系. [模板]扩展卢卡斯 不保证P是质数. $C_n^m=\frac{n!}{m!(n-m)!}$ 麻烦的是分母. 如果互 ...
- hdu 3037 费马小定理+逆元除法取模+Lucas定理
组合数学推推推最后,推得要求C(n+m,m)%p 其中n,m小于10^9,p小于1^5 用Lucas定理求(Lucas定理求nm较大时的组合数) 因为p数据较小可以直接阶乘打表求逆元 求逆元时,由费马 ...
- Lucas定理初探
1.1 问题引入 已知\(p\)是一质数,求\(\dbinom{n}{m}\pmod{p}\). 关于组合数,它和排列数都是组合数学中的重要概念.这里会张贴有关这两个数的部分内容. 由于Lucas定理 ...
- 【HDU 3037】Saving Beans Lucas定理模板
http://acm.hdu.edu.cn/showproblem.php?pid=3037 Lucas定理模板. 现在才写,noip滚粗前兆QAQ #include<cstdio> #i ...
- CF451E Devu and Flowers (隔板法 容斥原理 Lucas定理 求逆元)
Codeforces Round #258 (Div. 2) Devu and Flowers E. Devu and Flowers time limit per test 4 seconds me ...
随机推荐
- 《TCP/IP详解卷1:协议》第3章 IP:网际协议(1)-读书笔记
章节回顾: <TCP/IP详解卷1:协议>第1章 概述-读书笔记 <TCP/IP详解卷1:协议>第2章 链路层-读书笔记 <TCP/IP详解卷1:协议>第3章 IP ...
- Javascript基础系列之(四)数据类型 (数组 array)
字符串,数值,布尔值都属于离散值(scalar),如果某个变量是离散的,那么任何时候它只有一个值. 如果想使用变量存储一组值,就需要使用数组(array). 数组是由多个名称相同的树值构成的集合,集合 ...
- 自定义的 ListBoxItem 自适应ListBox的宽度
主要是要设置HorizontalContentAlignment的值,而不是HorizontalAlignment <ListBox x:Name="xxx"> < ...
- “耐撕”团队 2016.04.06 站立会议
1. 时间:20:00--20:20 共计20分钟. 2. 成员: Z 郑蕊 * 组长 (博客:http://www.cnblogs.com/zhengrui0452/), P 濮成林(博客:http ...
- Kettle_使用Pan.bat执行转换、Kitchen.bat执行作业
参考资料:http://www.cnblogs.com/wxjnew/p/3620792.html 注意:使用bat文件执行速度比执行在spoon.bat中执行慢很多 一.使用Pan.bat执行转换 ...
- 重写UIPageControl实现自定义按钮
有时候UIPageControl需要用到白色的背景, 那么会导致上面的点按钮看不见或不清楚,我们可以通过继承该类重写函数来更换点按钮的图片现实.实现思路如下.新建类继承UIPageControl : ...
- Intel 80x86 Linux Kernel Interrupt(中断)、Interrupt Priority、Interrupt nesting、Prohibit Things Whthin CPU In The Interrupt Off State
目录 . 引言 . Linux 中断的概念 . 中断处理流程 . Linux 中断相关的源代码分析 . Linux 硬件中断 . Linux 软中断 . 中断优先级 . CPU在关中断状态下编程要注意 ...
- c++ struct的两个注意点
1.C++的结构体变量在声明的时候可以省略struct,在c中这样是不可以的,例子如下 #include<iostream> #include<string> using na ...
- linux 下用户管理
linux 下用户管理 一.用户的分类 1.超级用户:root UID=0 2.系统用户:不需要登录系统,对应用程序服务,主要维护系统的正常运行:UID = 1 ~ 499(RHEL7 = 1 ~ 9 ...
- P问题、NP问题、NPC问题、NP难问题的概念
P问题.NP问题.NPC问题.NP难问题的概念 离入职尚有几天时间,闲来无事,将大家常见却又很容易搞糊涂的几个概念进行整理,希望对大家有所帮助.你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这 ...