路径规划 Adjacency matrix 传球问题

建模

问题是什么

知道了问题是什么答案就ok了

重复考虑 与 重复计算

程序可以重复考虑  但往目标篮子中放入时，放不放把握好就ok了。

集合

交集

并集

w

路径规划

字符串处理

42423
42424
42432
42434
43123
43124
43132
43134
43142
43143
43212
43213
43214
43232
43234
43242
43243
43412
43413
43414
43423
43424
43432
43434
183well@well:/home/etc/project$ cat w.php
<?php
$wx = 0;
$pass = array(11,22,33,44,5,6,7,8,9,0);
for($w=11111;$w<44445;$w++){
    $w.='';
    if(substr($w,0,1)!=1 && substr($w,strlen($w)-1,1)!=1)
    {    $flag=0;
        foreach($pass as $val){
            $val .='';
            if(strpos($w,$val)!==false)$flag = 1;
        }
        if($flag == 0){echo $w,"\n";$wx++;}
    }
    $w += 1-1;
}
echo $wx;

die();

https://en.wikipedia.org/wiki/Adjacency_matrix

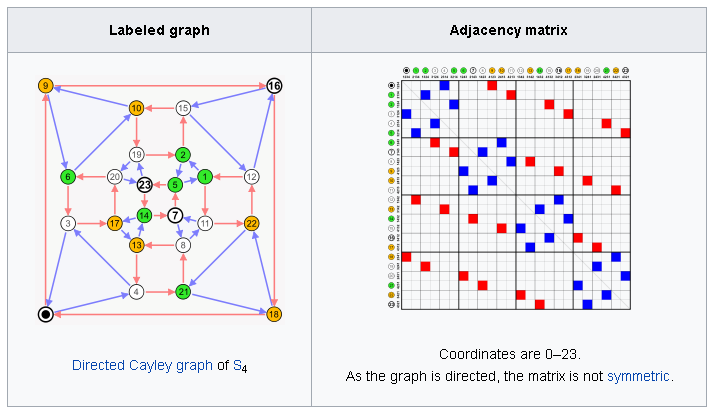
Undirected Graphs

The convention followed here (for undirected graphs) is that each edge adds 1 to the appropriate cell in the matrix, and each loop adds 2. This allows the degree of a vertex to be easily found by taking the sum of the values in either its respective row or column in the adjacency matrix.

Directed Graphs

In directed graphs, the in-degree of a vertex can be computed by summing the entries of the corresponding row, and the out-degree can be computed by summing the entries of the corresponding column.

w

传球问题的终极解法 吴炜超
http://old.pep.com.cn/rjwk/gzsxsxkj/2011/sxkj4/sxkj4ts/201106/t20110623_1050797.htm