POJ 3321 Apple Tree 【树状数组+建树】

Apple Tree

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 34812		Accepted: 10469

Description

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

Sample Output

3

2

Source

POJ Monthly--2007.08.05, Huang, Jinsong

题意概括：

给一个 N 阶无向图，要求把这个无向图转换为一颗以 1 为根的树后进行两种操作：

C x ：x结点上如果有苹果就摘掉，如果没有苹果就长出一个新的来

Q x: 查询 x 结点与它的所有后代分支一共有几个苹果

解题思路：

因为原本苹果之间的关系我们不好处理，所以就给他们这些结点重新编号。

并且为了方便子树的苹果数求和（即区间查询）我们在给结点增加一个左值一个右值表示当前结点管辖的范围。

如何建树？

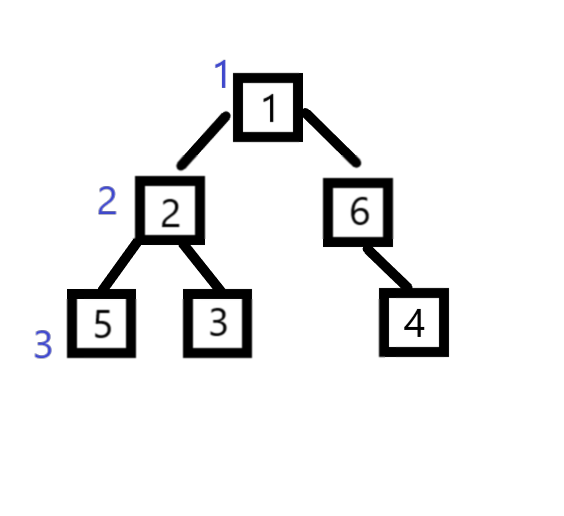
根据题目一开始给的边与边的关系我们可以通过 dfs 进行建树。

L[ x ] (X的左值）: X结点的新编号就是该结点的左值，表示它管辖范围的下限

R[ x ] (X的右值）：而子树的编号最大值为该结点的右值，表示它管辖范围的上限。

至于dfs顺序，如下

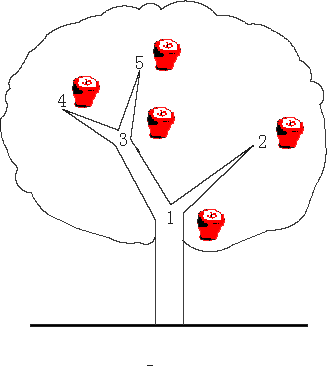
举个栗子：

N = 6；

1 - 2

1 - 6

2 - 5

2 - 3

6 - 4

到这里感觉有一点点线段树的味道了。。。

但这里要用树状数组对这些区间进行维护和查询。

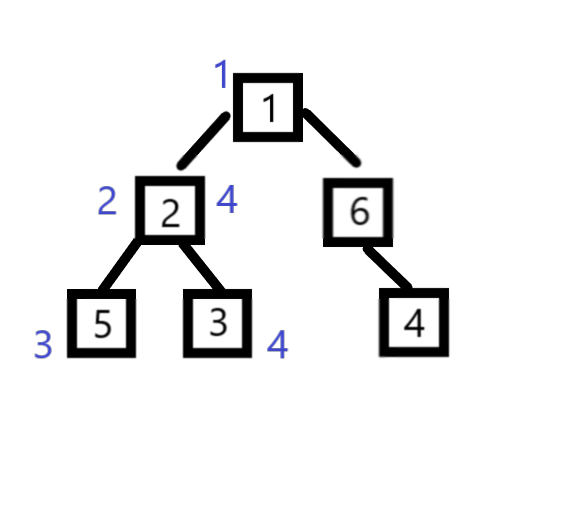
例如：我要 Q 2；

由上面建好的新树我们可以知道结点2这颗子树包含了结点2、结点5、结点3，而结点2所管辖的区间【2，4】刚好把它们包括进去了。

如果我们要求这可子树的苹果数量，其实就是用树状数组求区间【2，4】的苹果总数

也就是右值的前缀和减去左值的前缀和（但不包括左值，因为结点本身也要算进去）即：ans = sum( R[ 2 ] ) - sum( L[ 2 ] - 1);

而C操作其实就是树状数组的单点更新而已。

注意事项：

一开始用 stl 的 vector 存无向图，虽然过了但效率不咋地。想想好久没用静态邻接表了，换了一下，快了好多。

AC code：

 ///建树+树状数组（stl）8080k 1047ms

 /*

 #include <cstdio>

 #include <iostream>

 #include <cstring>

 #include <vector>

 #include <algorithm>

 #define INF 0x3f3f3f3f

 using namespace std;

 typedef vector<int>ve;

 const int MAXN  = 1e5+10;

 int t[MAXN], l[MAXN], r[MAXN];

 bool vis[MAXN];

 int N, M, cnt;

 vector<ve>node(MAXN);

 int lowbit(int x)

 {

     return x&(-x);

 }

 void add(int x, int value)

 {

     for(int i = x; i <= N; i+=lowbit(i))

         t[i]+=value;

 }

 int sum(int x)

 {

     int res = 0;

     for(int i = x; i > 0; i-=lowbit(i))

         res+=t[i];

     return res;

 }

 void dfs(int k)

 {

     l[k] = cnt;

     for(int i = 0; i < node[k].size(); i++)

     {

         cnt++;

         dfs(node[k][i]);

     }

     r[k] = cnt;

     return;

 }

 int main()

 {

     scanf("%d", &N);

     int a, b;

     for(int i = 1; i <= N; i++)

     {

         vis[i] = 1;

         add(i, 1);

     }

     for(int i = 1; i < N; i++)

     {

         scanf("%d%d", &a, &b);

         node[a].push_back(b);

     }

     cnt = 1;

     dfs(1);

     scanf("%d", &M);

     while(M--)

     {

         char com[3];

         int px;

         scanf("%s", &com);

         if(com[0] == 'C')

         {

             scanf("%d", &px);

             if(vis[px]) add(l[px], -1);

             else add(l[px], 1);

             vis[px] = !vis[px];

         }

         else

         {

             scanf("%d", &px);

             int ans = sum(r[px]) - sum(l[px]-1);

             printf("%d\n", ans);

         }

     }

     return 0;

 }

 */

 ///建树+树状数组（静态连接表） 4940k 454ms

 #include <cstdio>

 #include <iostream>

 #include <cstring>

 #include <vector>

 #include <algorithm>

 #define INF 0x3f3f3f3f

 using namespace std;

 const int MAXN = 1e5+;

 const int MAXM = 1e5+;

 struct node

 {

     int to, next;

 }edge[MAXM<<];

 int head[MAXN];

 bool vis[MAXN];

 int t[MAXN], l[MAXN], r[MAXN];

 int N, M, cnt, key;

 int lowbit(int x)

 {

     return x&(-x);

 }

 void add(int x, int value)

 {

     for(int i = x; i <= N; i+=lowbit(i))

         t[i]+=value;

 }

 int sum(int x)

 {

     int res = ;

     for(int i = x; i > ; i-=lowbit(i))

         res+=t[i];

     return res;

 }

 void dfs(int k)

 {

     l[k] = key;

     for(int i = head[k]; i != -; i = edge[i].next)

     {

         if(l[edge[i].to]) continue;

         key++;

         dfs(edge[i].to);

     }

     r[k] = key;

 }

 void init()

 {

     memset(head, -, sizeof(head));

     cnt = ;

 }

 void add_e(int u, int v)

 {

     edge[cnt].to = v;

     edge[cnt].next = head[u];

     head[u] = cnt++;

 }

 int main()

 {

     scanf("%d", &N);

     init();

     int a, b;

     for(int i = ; i <= N; i++)

     {

         vis[i] = ;             //每个节点一开始都有苹果

         add(i, );              //初始化树状数组

     }

     for(int i = ; i < N; i++)

     {

         scanf("%d%d", &a, &b); ///建无向图

         add_e(a, b);

         add_e(b, a);

     }

     key = ; dfs();           //建树

     scanf("%d", &M);

     int px;

     char com[];

     while(M--)

     {

         scanf("%s", &com);

         if(com[] == 'C')

         {

             scanf("%d", &px);

             if(vis[px]) add(l[px], -);

             else add(l[px], );

             vis[px] = !vis[px];

         }

         else

         {

             scanf("%d", &px);

             printf("%d\n", sum(r[px])-sum(l[px]-));

         }

     }

     return ;

 }