再回首数据结构—AVL树（一）

前面所讲的二叉搜索树有个比较严重致命的问题就是极端情况下当数据以排序好的顺序创建搜索树此时二叉搜索树将退化为链表结构因此性能也大幅度下降，因此为了解决此问题我们下面要介绍的与二叉搜索树非常类似的结构就诞生了；

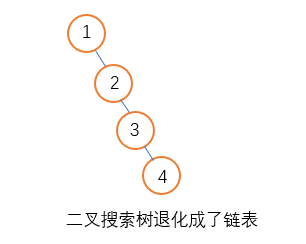
　　AVL（Adelson-Velskii and Landis）树，名字取自其发明者 G.M. Adelson-Velsky 和 E.M. Landis的首字母，AVL树是一棵特殊的二叉搜索树它与普通二叉搜索树最主要的区别就是其能够使二叉搜索树维持其左右节点的平衡；

　　AVL树：其任意一个节点左子树与右子树高度差不超过1，由于此特征因此需要在AVL增删节点时维护其左右节点使该树满足该特性（左右节点平衡）；

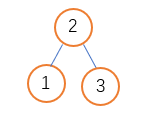
　　此AVL树中节点2节点高度都为2，节点1与3节点高度都为1；节点高度为左右子树中最大的节点高度+1；

AVL树实现关键

　　1、标注其节点高度

　　2、计算节点平衡因子

　　3、维护其节点满足左右节点高度不超过1

AVL树的实现

　　1、AVL树定义

　　根据AVL树的特性先定义该数据类型的结构；

 type AVL struct {
   root    *AVLNode
   size    int
   compare Comparable
 }
 type AVLNode struct {
   e      interface{}
   left   *AVLNode
   right  *AVLNode
   height int
 }

　　AVL：为定义的AVL树自定义对象

　　AVLNode：为树中每个节点的节点自定义对象

　　compare：为定义的用于树中节点元素进行数据对比的对象

　　size：AVL树的元素个数

　　root：树的根节点

　　e：节点元素值

　　left：左子树

　　right：右子树

　　height：节点高度

　　AVL树与二叉搜索树一样所有很多操作都可用递归来实现，比如元素的添加、删除、查找等；

　　可以说AVL树为二叉搜索树的升级版本所以并不会像出现二叉搜索树一样出现退化为O(n)时间复杂度的情况，与二叉搜索树一样通过中序遍历可得到排序好的数据，二叉搜索树的搜索、插入、删除时间复杂度为O(log(n))，n为树的深度，这里只是简单的介绍了AVL树，后面会有AVL树实现的相关介绍；

文章首发地址：Solinx

http://www.solinx.co/archives/1323